Производная сложной функции

Рассмотрим сложную функцию . Теорема: если   имеет в точке   производную   и  имеет в точке  производную , то сложная функция F [ f (x)] имеет в точке  производную, равную произведению .

Правило дифференцирования сложных функций. Производная сложной функции Z = F [ f (x)] равна производной данной функции Z по промежуточной переменной , умноженной на производную от промежуточной переменной  по независимой переменной x, т.е.    или        , .

 2.2.6 Производная обратной функции

Пусть  есть дифференцируемая функция от аргумента
 в некотором интервале . Если в данном уравнении  рассматривать как независимую переменную, а  как функцию и при выбранных значениях  из этого уравнения  определяется однозначно, то получится новая функция , называемая обратной по отношению к данной. При этом справедливо тождество f [j(y)] = y.

Теорема: если  имеет в точке  производную , отличную от нуля, то обратная функция j(y) имеет в точке  производную .

Правило дифференцирования обратных функций. Производная обратной функции равна единице, деленной на производную первоначальной функции в соответствующей точке.

Производная неявной функции

Пусть функция  задана уравнением как неявная функция от 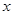. Продифференцируем левую часть уравнения по , считая  функцией от , используя правило дифференцирования сложной функции. Приравняв нулю полученное выражение, выразим из него производную .