2020-05-25
173
Если C — постоянная, то dC = 0, т.е. дифференциал постоянной равен нулю.
Дифференциал суммы равен сумме дифференциалов слагаемых:
.
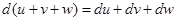Постоянный множитель можно выносить за знак дифференциала: 
.
Дифференциал произведения 
.
Дифференциал частного 
.
Дифференциал сложной функции имеет тот же вид, что имел бы
в том случае, если бы вспомогательная функция 
была независимой переменной, т.е.
, 
, 
.
2.4.4 Приближенное вычисление с помощью дифференциала
Во многих задачах приращение функции в данной точке 
приближенно заменяют дифференциалом функции в этой точке 
.
Абсолютная погрешность при такой замене равна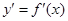 
и при
D x ® 0 является бесконечно малой более высокого порядка, чем D x. Приращенное значение вычисляют по формуле 
.
Производные и дифференциалы высших порядков
2.5.1 Производная n -го порядка
Производная 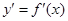функции 
сама является некоторой функцией аргумента x. Производная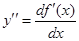 
от производной 
называется производной второго порядка от функции f (x). Производная n - го порядка является производной от (n – 1)-го порядка, т.е. 
.
|
|
|
Обозначаются производные высших порядков, начиная со второй, следующим образом: 
, 
,.., 
или 
, 
, …, 
, или 
, …, 
.
Если 
описывает закон движения материальной точки по прямой линии, то первая производная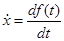 
есть мгновенная скорость точки в момент времени 
, а вторая производная 
равна изменению скорости, т.е. ускорению движущейся точки в этот момент.
2.5.2 Дифференциалы высших порядков
Дифференциал 
функции 
первого порядка является функцией двух переменных: аргумента 
и его дифференциала 
. Если производная 
дифференцируема в некоторой точке х, тогда можно рассматривать в 
как постоянный множитель, а 
как функцию только аргумента х. Дифференциал от этой функции называется дифференциалом второго порядка:
; 
.
Дифференциал n -го порядка определяется формулой 
.
Основные теоремы дифференциального исчисления
Теорема Ферма
Пусть функция 
определена на интервале 
и в некоторой точке 
этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке 
существует производная, то она равна нулю, т.е. 
.
Геометрический смысл теоремы Ферма. Если в точке 
дифференцируемая функция имеет наибольшее или наименьшее значение, то в точке 
касательная к графику функции 
параллельна оси OХ (рис. 4.3).
