Производная постоянной величины

Если , где 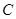 — постоянная величина, то . Иными словами, производная постоянной величины равна нулю.

Производная суммы

Если , то . Иными словами, производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций.

 2.2.3 Производная произведения

Если , то . Иными словами,производная произведения двух дифференцируемых функций равна произведению первого сомножителя на производную второго плюс произведение второго на производную первого.

Если , то .

Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на остальные. Если , то

.

 2.2.4 Производная частного. Если числитель и знаменатель — дифференцируемые функции и знаменатель не обращается в нуль, то производная дроби (частного) равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, все разделенное на квадрат знаменателя. Если , то .   Если , то .