Определение дифференциала

Дифференциалом функции называется величина, пропорциональная приращению независимой переменной и отличающаяся от приращения функции на бесконечно малую величину высшего порядка малости по сравнению с приращением независимой переменной.

Напомним, что функция называется дифференцируемой
в точке, если ее приращение 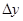в этой точке можно представить в виде

Слагаемое в данной формуле называют главной линейной частью приращения функции.

Дифференциал функции в точке представляет собой главную, линейную относительно часть бесконечно малого приращения функции в этой точке .

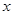Учитывая, что равно производной , вычисленной в точке , предыдущую формулу можно записать в виде .

Пусть , тогда . Дифференциалом независимой переменной 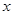является ее приращение . Таким образом, получаем .

Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

2.4.2 Геометрический смысл дифференциала

Дифференциал функции в точке равен приращению ординаты касательной MS к графику этой функции в точке , тогда как приращение функции есть приращение ординаты самой функции в точке , соответствующее приращению аргумента (рис. 4.2).