Пусть даны две функции  ,
,  одной независимой переменной t, определенные и непрерывные в одном и том же промежутке. Если
одной независимой переменной t, определенные и непрерывные в одном и том же промежутке. Если  строго монотонна, то обратная к ней функция
строго монотонна, то обратная к ней функция  однозначна, также непрерывна и строго монотонна. Поэтому
однозначна, также непрерывна и строго монотонна. Поэтому 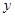 можно рассматривать как функцию, зависимую от переменной
можно рассматривать как функцию, зависимую от переменной  посредством переменной t, называемой параметром:
посредством переменной t, называемой параметром:  ,Функция
,Функция  непрерывна в силу теоремы о непрерывности сложной функции.
непрерывна в силу теоремы о непрерывности сложной функции.
Теорема: если функция  от аргумента
от аргумента  задана параметрически уравнением x = j(t), y = y(t), где j(t) и y(t) дифференцируемы и c ¹ 0, то производная этой функции равна
задана параметрически уравнением x = j(t), y = y(t), где j(t) и y(t) дифференцируемы и c ¹ 0, то производная этой функции равна  .
.
Таблица производных для основных элементарных функций
Дифференцирование сложной функции. Пусть Тогда |
Дифференциал функции
 2020-05-25
2020-05-25 154
154






 ;
; 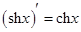 Основные правила дифференцирования
Основные правила дифференцирования

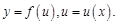
 или
или 







