2020-05-25
97
Пусть функция 
от независимых переменных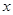 
и 
задана уравнением 
где 
— дифференцируемая функция. Тогда частные производные функции по переменным х и могут быть вычислены по формулам: 
; 
, при условии, что 
.
Пример 1. Найти частные производные функции: 
.
Решение: 
(производная второго слагаемого равна нулю как производная константы)
.
Пример 2. Найти частные производные функции: 
.
Решение: 
.
Пример 3. Найти частные производные функции: 
.
Решение: Частная производная по переменной 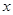является производной степенной функции с фиксированным показателем ; поэтому 
.
Частная производная по переменной является производной показательной функции с фиксированным основанием 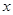; поэтому 
.
Пример 4. Найти частные производные функции: 
.
Решение: По правилу дифференцирования сложной функции:
;
.
Пример 5. Найти полный дифференциал функции: 
Решение: Найдем производные первого порядка. Вычисляя производную по 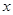, полагаем постоянным:
так как 
и 
, то выражение 
Аналогично, вычисляя производную по , полагаем 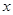постоянным: 
|
|
|
так как 
и 
, то выражение 
.
Выпишем получившиеся производные: 
, 
Подставим их в формулу полного дифференциала (3), получаем
Пример 6. Найти частные производные второго порядка функции:
.
Решение: Частные производные первого порядка имеют вид
, 
.
Считая их новыми функциями двух переменных, найдем их частные производные. Получаем: 
,
,
.
Ø Обратите внимание! Мы нашли только три частные производные второго порядка, так как смешанные производные равны между собой, если они непрерывны.
Проверим это утверждение на нашем примере. Функция и все ее производные непрерывны на 
. Найдем вторую смешанную производную:
Мы получили 
.
