Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную 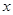 , искомую функцию
, искомую функцию  и ее производные
и ее производные  , т. е. уравнение вида
, т. е. уравнение вида
 . (1)
. (1)
Решением дифференциального уравнения называется такая дифференцируемая функция  , которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество.
, которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Пример 1. Доказать, что функция  является решением дифференциального уравнения
является решением дифференциального уравнения  .
.
Решение. По определению решения достаточно показать, что при подстановке в уравнение, функция  обращает его в тождество.
обращает его в тождество.
Уравнение  — дифференциальное уравнение первого порядка, поэтому необходимо найти только первую производную функции
— дифференциальное уравнение первого порядка, поэтому необходимо найти только первую производную функции
 .
.
Подставим  и
и  в уравнение
в уравнение  :
:
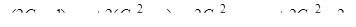 .
.
Следовательно, функция  является решением дифференциального уравнения
является решением дифференциального уравнения  при любых значениях С.
при любых значениях С. 
Пример 2. Доказать, что функция  является решением дифференциального уравнения
является решением дифференциального уравнения  .
.
Решение. Чтобы подставить функцию  в дифференциальное уравнение второго порядка, необходимо найти ее первую и вторую производную:
в дифференциальное уравнение второго порядка, необходимо найти ее первую и вторую производную:
 ,
,  ,
,  .
.
Подставим  ,
,  ,
,  в уравнение
в уравнение  :
:
 ;
;  .
.
Следовательно, функция  является решением дифференциального уравнения
является решением дифференциального уравнения  .
.
Дифференциальным уравнением первого порядка называется уравнение вида
 (2)
(2)
или  , (3)
, (3)
где  — неизвестная функция переменной
— неизвестная функция переменной 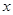 . Дифференциальное уравнение (3) называют дифференциальным уравнением первого порядка, разрешенным относительно производной. Оно может быть записано в дифференциалах
. Дифференциальное уравнение (3) называют дифференциальным уравнением первого порядка, разрешенным относительно производной. Оно может быть записано в дифференциалах
 . (4)
. (4)
Для этого надо в уравнении (3) 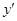 заменить на
заменить на  и выполнить тождественные преобразования. Например, уравнение
и выполнить тождественные преобразования. Например, уравнение  является уравнением вида (3). Выполним указанные преобразования:
является уравнением вида (3). Выполним указанные преобразования:
 по свойству пропорций
по свойству пропорций 
 . (4)
. (4)
Получили уравнение в дифференциалах вида (4).
Как правило, дифференциальное уравнение имеет не одно, а множество решений (см. пример 1).
Общим решением дифференциального уравнения первого порядка в области  называется функция
называется функция 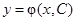 , обладающая следующими свойствами:
, обладающая следующими свойствами:
1) она является решением данного уравнения при любых значениях произвольной постоянной 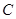 ;
;
2) для любого условия  при
при  , т. е.
, т. е.  , такого, что
, такого, что  , существует единственное значение
, существует единственное значение  , при котором решение
, при котором решение 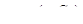 удовлетворяет заданному условию.
удовлетворяет заданному условию.
Равенство  , неявно задающее общее решение, называется общим интегралом дифференциального уравнения.
, неявно задающее общее решение, называется общим интегралом дифференциального уравнения.
Частным решением дифференциального уравнения называется любая функция 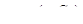 , которая получается из общего решения при конкретном значении
, которая получается из общего решения при конкретном значении  (функция
(функция  называется частным интегралом).
называется частным интегралом).
Задача, в которой требуется найти частное решение (частный интеграл) дифференциального уравнения, удовлетворяющее условию  при
при  (или
(или  ), называется начальной задачей или задачей Коши. Условия
), называется начальной задачей или задачей Коши. Условия  при
при  принято называть начальными условиями.
принято называть начальными условиями.
Построенный на плоскости 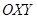 график любого решения
график любого решения  (или интеграла) дифференциального уравнения называется интегральной кривой. Общему решению дифференциального уравнения первого порядка
(или интеграла) дифференциального уравнения называется интегральной кривой. Общему решению дифференциального уравнения первого порядка  на плоскости
на плоскости 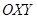 соответствует семейство интегральных кривых, зависящих от одного параметра — произвольной постоянной
соответствует семейство интегральных кривых, зависящих от одного параметра — произвольной постоянной 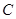 , а частному решению
, а частному решению 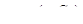 , удовлетворяющему начальному условию
, удовлетворяющему начальному условию  — кривая этого семейства, проходящая через заданную точку
— кривая этого семейства, проходящая через заданную точку  .
.
7.2. Дифференциальные уравнения первого порядка
с разделяющимися переменными
Дифференциальным уравнением первого порядка с разделяющимися переменными называется уравнение, которое может быть представлено в виде
 (5)
(5)
или в виде
 , (6)
, (6)
где 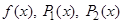 — некоторые функции, зависящие только от переменной
— некоторые функции, зависящие только от переменной 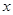 , а
, а  — функции от переменной
— функции от переменной  .
.
Для того чтобы решить уравнение (5), его сначала приводят к виду (6), а затем с помощью тождественных преобразований добиваются того, что дифференциал и функции переменной 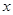 окажутся в одной части равенства, а дифференциал и функции переменной
окажутся в одной части равенства, а дифференциал и функции переменной  — в другой. Уравнение (6) преобразуют следующим образом:
— в другой. Уравнение (6) преобразуют следующим образом:
 .
.
Предполагая, что 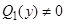 и
и  , разделим правую и левую части равенства на
, разделим правую и левую части равенства на  . Получим уравнение
. Получим уравнение
 . (7)
. (7)
Затем интегрируем левую и правую части равенства
 .
.
Пример 3. Найти общее решение дифференциального уравнения первого порядка  . Найти частное решение, удовлетворяющее начальным условиям
. Найти частное решение, удовлетворяющее начальным условиям  при
при 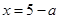 , привести примеры других частных решений.
, привести примеры других частных решений.
Решение. Решим задачу для значений параметров  ,
,  . Уравнение и начальные условия будут иметь вид:
. Уравнение и начальные условия будут иметь вид:  ,
,  при
при  . Данное уравнение — это дифференциальное уравнение с разделяющимися переменными, так как его можно привести к виду:
. Данное уравнение — это дифференциальное уравнение с разделяющимися переменными, так как его можно привести к виду:

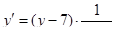 .
.
Сравнивая с (5), видим, что это уравнение с разделяющимися переменными. Заменим в уравнении 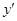 на
на  , получим
, получим  . Разделим переменные и проинтегрируем:
. Разделим переменные и проинтегрируем:
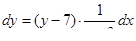 ;
;  ;
;


 .
.
Замечание. Произвольная постоянная 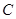 не меняется при делении или умножении на любое число, отличное от нуля. Кроме того, чтобы упростить данное выражение, можно записать произвольную постоянную
не меняется при делении или умножении на любое число, отличное от нуля. Кроме того, чтобы упростить данное выражение, можно записать произвольную постоянную 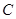 в виде
в виде 
 .
.
Используя известную формулу логарифмирования
 ,
,
получим
 ,
,  ,
, 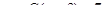 .
.
Мы нашли общее решение уравнения
 .
.
Чтобы найти частное решение, найдем  , отвечающее заданным начальным условиям. Для этого подставим в общее решение
, отвечающее заданным начальным условиям. Для этого подставим в общее решение  и
и  :
:
 ;
;  ;
;  .
.
Подставим найденное  в формулу общего решения:
в формулу общего решения:
 или
или  .
.
Это частное решение дифференциального уравнения, удовлетворяющее начальным условиям, следовательно, мы нашли решение задачи Коши.
Составим уравнения интегральных кривых при различных значениях произвольной постоянной 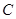 :
:
 ;
; 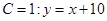 ;
;  ;
;  .
.
Мы получили семейство интегральных кривых. Оно состоит из прямых линий.
Решением задачи Коши является прямая, проходящая через точку  .
.
 2020-05-25
2020-05-25 499
499








