Задание 22. Вычислить несобственный интеграл.
1.  . .
| 2.  . .
|
3.  . .
| 4.  . .
|
5. 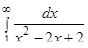 . .
| 6.  . .
|
7. 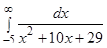 . .
| 8.  . .
|
9.  . .
| 10. 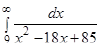 . .
|
Задание 23. Вычислитьнесобственный интеграл или доказать его расходимость 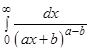 .
.
| № варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| a | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| b | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Цель курса. Изучение функкций нескольких переменных, включая их жифференцирование и исследование на экстремум.
6.1. Частные производные
Линией уровня функции u = f (x, y) называется линия f (x, y) = C на плоскости Oxy, в точках которой функция 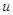 сохраняет постоянное значение C = const.
сохраняет постоянное значение C = const.
Поверхностью уровня функции u = f (x, y, z) называется поверхность f (x, y, z) = C, в точках которой функция 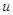 сохраняет постоянное значение C = const.
сохраняет постоянное значение C = const.
Частной производной от функции 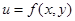 по независимой переменной
по независимой переменной 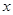 называется конечный предел
называется конечный предел
 ,вычисленный при постоянном
,вычисленный при постоянном  .
.
Частной производной по переменной  называется конечный предел
называется конечный предел
 ,вычисленный при постоянном
,вычисленный при постоянном 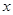 .Для частных производных справедливы обычные правила и формулы дифференцирования.
.Для частных производных справедливы обычные правила и формулы дифференцирования.
Применяются следующие обозначения:  ,
,  .
. 
Полный дифференциал
Полным приращением функции u = f (x, y) в точке M(x, y) называется разность
 ,
,
где 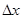 и
и 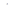 — произвольные приращения аргументов.
— произвольные приращения аргументов.
Функция u = f (x, y) называется дифференцируемой в точке f (x 0, y 0), если в этой точке полное приращение можно представить в виде  , где
, где  и
и  — постоянные (зависящие от координат точки (x 0, y 0)).
— постоянные (зависящие от координат точки (x 0, y 0)).
Полным дифференциалом функции u = f (x, y) называется главная часть полного приращения 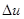 , линейная относительно приращений аргументов
, линейная относительно приращений аргументов 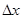 и
и  , т.е.
, т.е. 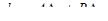 .
.
Полный дифференциал функции u = f (x, y) вычисляется по формуле  .
.
Аналогично полный дифференциал функции трех аргументов  вычисляется по формуле
вычисляется по формуле  .
.
При достаточно малой величине  для дифференцируемой функции
для дифференцируемой функции 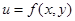 справедливы приближенные равенства
справедливы приближенные равенства
 и
и  .
.
 2020-05-25
2020-05-25 104
104








