Частные производные, определенные в пункте 11.1.1, называются также частными производными первого порядка от функции 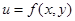 .
.
Частными производными второго порядка от функции 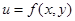 называются частные производные от ее частных производных первого порядка.
называются частные производные от ее частных производных первого порядка.
Обозначения частных производных второго порядка:
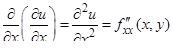 ;
; 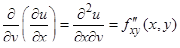 ;
;
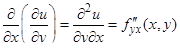 ;
; 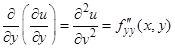
и т.д.
Смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны: 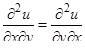 .
.
Дифференциалом второго порядка от функции 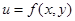 называется дифференциал от ее полного дифференциала, т.е.
называется дифференциал от ее полного дифференциала, т.е. 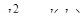 .
.
Аналогично определяются дифференциалы третьего и высших порядков: 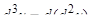 ,
, 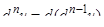 .
.
Если 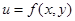 имеет непрерывные частные производные, то имеем
имеет непрерывные частные производные, то имеем
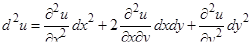 ;
;
Дифференцирование сложных функций
Пусть 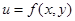 , где
, где 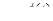 и
и 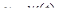 . Тогда производная по переменной t функции
. Тогда производная по переменной t функции 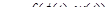 вычисляется по формуле
вычисляется по формуле 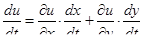 .
.
Если 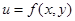 , где
, где 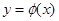 , то
, то 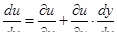 .
.
Если 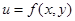 , где
, где 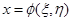 ,
, 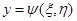 , то
, то
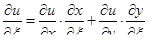 ,
, 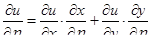 .
.
 2020-05-25
2020-05-25 140
140








