Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Уравнение вида  ,              (15)

где  — некоторые функции переменной x, называют линейным однородным дифференциальным уравнением второго порядка. Оно линейно относительно . Если , — постоянные, то уравнение называют линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.

                                      .                  (16)

Общее решение уравнения (16) имеет вид ,

где  и  — линейно независимые (т. е. образуют фундаментальную систему решений) решения этого уравнения. Для того, чтобы найти  и  составляют характеристическое уравнение                                .                   (17)

В зависимости от дискриминанта этого уравнения, а, следовательно, от вида его корней, соответствующее дифференциальное уравнение (16) имеет фундаментальную систему решений  и     и общее решение  , указанные в табл. 1.

Замечание. При решении квадратного уравнения  вычисляют дискриминант . Возможны три случая:

–  — уравнение имеет два действительных различных корня ;

–  — уравнение имеет один действительный корень  (говорят, что это корень кратности 2);

–  — уравнение имеет два комплексных корня 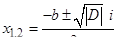, где .

Таблица 1

Решения линейного однородного дифференциального уравнения

второго порядка с постоянными коэффициентами

	Корни характеристического уравнения	Фундаментальная система решений	Общее решение
	— действительные различные
	— действительные равные
	– комплексные

Пример 6. Найти общее решение уравнения:

1) ; 2) ; 3) .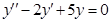

Решение.

1) . Составим характеристическое уравнение:

.

Решим полученное квадратное уравнение:

; , откуда

; .

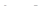Следовательно, общее решение (табл. 1) имеет вид

.

2) . Характеристическое уравнение ,

; . Следовательно, общее решение (табл. 1) имеет вид .

3) 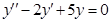. Характеристическое уравнение ,

, корни комплексные, ,

, откуда  и .

Следовательно, общее решение (табл. 1) имеет вид:

.

Пример 7. Найти общее решение дифференциального уравнения  и частное решение, удовлетворяющее начальным условиям .

Решение. Решим эту задачу для значений параметров a= 3, b= 7. Уравнение и начальные условия будут иметь вид . Характеристическое уравнение  имеет корни ; . Следовательно, . По табл. 1 находим общее решение

.

Теперь можно найти частное решение, удовлетворяющее заданным начальным условиям. Для этого продифференцируем общее решение

.

Подставим начальные условия в найденное общее решение и его производную:

;

.

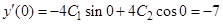Решаем систему уравнений, находим

, .

Подставляем найденные значения  в общее решение

.

Получили частное решение, удовлетворяющее заданным начальным условиям.