Функция  называется однородной p-го измерения относительно
называется однородной p-го измерения относительно 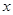 и
и  , если для любого
, если для любого 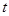 выполняется равенство
выполняется равенство
 . (8)
. (8)
Из определения следует, что функция  является однородной функцией измерения 2, так как
является однородной функцией измерения 2, так как
 .
.
В частности, если  , то
, то  называют однородной функцией нулевого измерения. Для таких функций соотношение (8) принимает вид
называют однородной функцией нулевого измерения. Для таких функций соотношение (8) принимает вид
 . (9)
. (9)
Например, функция  является однородной функцией нулевого измерения, так как
является однородной функцией нулевого измерения, так как
 .
.
Дифференциальное уравнение первого порядка вида  называется однородным, если его правая часть
называется однородным, если его правая часть  есть однородная функция нулевого измерения.
есть однородная функция нулевого измерения.
Доказано, что однородная функция нулевого измерения зависит не от двух переменных 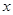 и
и  , а только от их отношения
, а только от их отношения  . Поэтому однородные дифференциальные уравнения решают с помощью подстановки
. Поэтому однородные дифференциальные уравнения решают с помощью подстановки



где  — новая неизвестная функция. Относительно
— новая неизвестная функция. Относительно  дифференциальное уравнение является уравнением с разделяющимися переменными.
дифференциальное уравнение является уравнением с разделяющимися переменными.
Пример 4. Решить уравнение  .
.
Решение. Уравнение  является однородным, так как его правая часть является однородной функцией нулевого измерения (см. пример выше). Сделаем подстановку:
является однородным, так как его правая часть является однородной функцией нулевого измерения (см. пример выше). Сделаем подстановку:
 ,
,  ,
,  ,тогда
,тогда  ;
;  ;
;  .
.
Это уравнение с разделяющимися переменными. Разделим переменные, для этого заменим  на
на  :
:  ;
;  ;
;  .
.
Интегрируя, получаем  ,
,  .
.
Вернемся к искомой функции  . Так как
. Так как  , имеем
, имеем  ;
;  — общее решение дифференциального уравнения.
— общее решение дифференциального уравнения.
Линейным дифференциальным уравнением первого порядка называется уравнение, которое может быть приведено к виду
 , (10)
, (10)
где  — заданные функции переменной
— заданные функции переменной 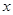 . Уравнение (10) линейно относительно
. Уравнение (10) линейно относительно  и
и 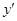 .Решение линейного уравнения 1-го порядка находят в виде произведения двух функций
.Решение линейного уравнения 1-го порядка находят в виде произведения двух функций
 (11)
(11)
где  ,
,  — неизвестные дифференцируемые функции.
— неизвестные дифференцируемые функции.
После замены (11) решение уравнения (10) сводится к решению двух дифференциальных уравнений с разделяющимися переменными вида (5):
 (12)
(12)
Пример 5. Найти общее решение дифференциального уравнения  .
.
Решение. Это уравнение линейно относительно  и
и 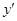 . Приведем его к виду (10). Для этого разделим правую и левую части на
. Приведем его к виду (10). Для этого разделим правую и левую части на 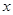 :
:  .
.
Здесь  ,
,  . Введем замену (11)
. Введем замену (11)  :
:
 или
или  .
.
Приравнивая к нулю выражение в скобках, получаем первое уравнение системы (12), остальные члены равенства образуют второе уравнение. При этом каждое уравнение является уравнением 1-го порядка вида (5), т. е. с разделяющимися переменными.
 (*)
(*)
Решим первое уравнение системы (*):
 ;
;  ;
;  ;
;
 ;
;  .Поскольку в данном случае достаточно найти одно из решений этого уравнения, которое обращает скобку в ноль, то обычно полагают
.Поскольку в данном случае достаточно найти одно из решений этого уравнения, которое обращает скобку в ноль, то обычно полагают  . Тогда
. Тогда  ;
;  ;
;  .
.
Замечание. Здесь использовано свойство логарифма  .
.
Подставим  во второе уравнение системы (*), получим уравнение с разделяющимися переменными:
во второе уравнение системы (*), получим уравнение с разделяющимися переменными:
 ;
;  ;
;  .
.
Интегрируем последнее равенство
 ;
;  ;
;  .
.
Поскольку  , то
, то  — общее решение исходного дифференциального уравнения.
— общее решение исходного дифференциального уравнения.
 2020-05-25
2020-05-25 133
133








