2020-05-25
94
Дифференциальным уравнением второго порядка называется уравнение вида
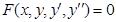. (13)
Решением такого дифференциального уравнения называется дважды дифференцируемая функция 
, которая обращает данное уравнение в тождество.
Задача Коши для уравнения второго порядка состоит в том, чтобы найти решение уравнения (13), удовлетворяющее условиям 
, 
при 
, где 
, 
, 
— заданные числа, которые называются начальными данными или начальными условиями. Начальные условия могут быть записаны в виде:
; 
. (14)
Общим решением дифференциального уравнения второго порядка в области 
называется функция 
, обладающая следующими свойствами:
1) она является решением данного уравнения при любых значениях произвольных постоянных 
;
2) для любых условий , 
при , (или , ) таких, что 
, существуют единственные значения 
, при которых решение 
удовлетворяет заданным условиям.
Всякое решение, получаемое из общего решения при конкретных значениях постоянных , 
, называется частным решением уравнения (13).
|
|
|
Интегрирование дифференциальных уравнений второго порядка (в конечном виде) удается провести только в некоторых частных случаях. Рассмотрим некоторые из них.
