Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами
 , (18)
, (18)
где  ,
,  — постоянные, а
— постоянные, а  — функция специального вида. Из теории известно, что общее решение неоднородного дифференциального уравнения (18) имеет вид
— функция специального вида. Из теории известно, что общее решение неоднородного дифференциального уравнения (18) имеет вид
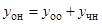 , (19)
, (19)
где  — общее решение неоднородного уравнения (18);
— общее решение неоднородного уравнения (18);
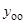 — общее решение однородного уравнения
— общее решение однородного уравнения  , соответствующего уравнению (18), когда
, соответствующего уравнению (18), когда  ;
;
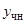 — частное решение неоднородного уравнения (18).
— частное решение неоднородного уравнения (18).
Укажем вид частного решения 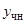 уравнения (18), если
уравнения (18), если  имеет специальный вид
имеет специальный вид
 , (20)
, (20)
где a, b — вещественные числа;  ,
,  — многочлены соответственно степеней
— многочлены соответственно степеней 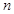 и
и  .
.
Замечание. Многочлены нулевой, первой и второй степени имеют вид:
 ;
;  ;
;  и т. д.
и т. д.
Составим контрольное число  .
.
1. Если число  не является корнем характеристического уравнения, т. е.
не является корнем характеристического уравнения, т. е.

 , (21)
, (21)
где 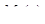 и
и  — многочлены степени
— многочлены степени  с неизвестными коэффициентами.
с неизвестными коэффициентами.
2. Если число  есть корень характеристического уравнения кратности 1, т. е. совпадает только с одним из корней характеристического уравнения
есть корень характеристического уравнения кратности 1, т. е. совпадает только с одним из корней характеристического уравнения
 ,
, 
 . (22)
. (22)
3. Если число  есть корень характеристического уравнения кратности 2, т. е.
есть корень характеристического уравнения кратности 2, т. е.

 . (23)
. (23)
 2020-05-25
2020-05-25 119
119








