2020-05-25
1304
Для обратимой реакции, где все реагенты идеальные газы
,
согласно закону действующих масс, выразим константу равновесия через равновесные концентрации реагентов. Концентрационная константа – эмпирическая константа равновесия равна
, где сi – равновесная молярная концентрация.
Размерность константы: [ 
] и др.
Для идеальных газов константу можно выразить через равновесные парциальные давления
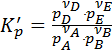, где pi – равновесное парциальное давление.
Размерность константы: [ 
Используя уравнение Менделеева-Клапейрона, выведем уравнение, связывающее эти выражения:
; 
; 
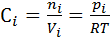Или 
Константу равновесия можно выразить через равновесную мольную долю (xi) или через равновесное число моль реагентов (ni):
; 
;
С учётом того, что: pi = xi×p (закон Дальтона для ид. газов)
И 
Получим следующие уравнения:
Где 
.
Для реальных газов константа равновесия может быть выражена через равновесные фугитивности (летучести)
Где 
- равновесная фугитивность (летучесть) i-того газа.
Летучесть связана с давлением уравнением:
f = g×р
g - коэффициент летучести (фугитивности).
Коэффициент летучести это мера отклонения поведения реального газа от идеального. При низких давлениях коэффициент летучести равен 1, и газ можно считать идеальным.
Если реакция протекает в конденсированных средах, например, в растворах, то константа равновесия должна быть выражена через активности.
Где ai – активность i-того компонента. Активность равна 
, где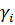 
- коэффициент активности. Активность безразмерная величина и константа, выраженная через активности, является термодинамической константой. Для идеальных растворов 
, тогда будет справедлива концентрационная константа.
