Энергия Гиббса и константа равновесия

В химической термодинамике имеется соотношение, которое связывает энергию Гиббса с константой равновесия. Это широко известное уравнение Вант-Гоффа, которое записывается в ленейном и экспотенциальном виде:

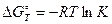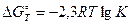
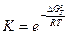или

или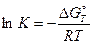

Рассчитав величину DG⁰₂₉₈ химической реакции, можно определить константу равновесия. Из уравнения (4.13) следует, что если величина DG⁰ отрицательна, то lgК должен быть положительным, что, в свою очередь, означает, что К >1. И наоборот, если DG⁰ > 0, то К <1.

Пример 13. Прямая или обратная реакция будет протекать при стандартных условиях в системе:

CH_4(г) + СО_{2 (г)} 2СО _(г) + 2Н_{2 (г)}.

Запишите закон действия масс для этой реакции.

Решение: Для ответа на вопрос следует вычислить DG⁰₂₉₈ или 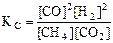 прямой реакции. Последнее выражение и есть ЗДМ. Значения DG⁰₂₉₈ соответствующих веществ приведены в таблице 4.1. Зная, что значения DG⁰_f для простых веществ, находящихся в устойчивых при стандартных условиях агрегатных состояниях, равны нулю, а значения DG⁰_ƒ (в кДж/моль) для СO₂ (-394,3), СН₄ (-50,8) и СО (-137,1), используя уравнение (4.7), рассчитываем DG⁰_х.р.:

DG⁰_х..р. = 2DG⁰_ƒ,(СО) - DG⁰_ƒ, (СН₄) - DG⁰_ƒ, (СО₂) = 2·(-137,1) - (-50,8 - 394,3) = +170,9 кДж = 170900 Дж.

После этого вычисляем константу равновесия

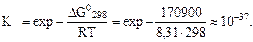
То, что DG > 0, а Kр << 1, указывает на невозможность самопроизвольного протекания прямой реакции при T = 298 К и равенстве давлений взятых газов
1,013 × 10⁵ Па (760 мм рт.ст. или 1 атм.). Самопроизвольно при этих условиях будет протекать обратная реакция, т.к. для нее DG = -170,9 кДж, а К» 10³⁷.

Пример 14. На основании стандартных энтальпий образования и абсолютных стандартных энтропий веществ (табл. 4.1) вычислите DG⁰₂₉₈ реакции, протекающей по уравнению

CO_(г) + Н₂О_(ж) СО_{2 (г)} + Н_{2 (г)}, DН⁰_ƒ, (кДж/моль) -110,5 -285,8 -393,5 0S⁰ (Дж/моль · К) 197,5 70,1 213,6 130,6

Запишите закон действующих масс и вычислите Kp.

Решение:

1) DН⁰ = (-393,5 + 0) - (-110,5 - 285,8) = + 2,80 кДж.

2) DS⁰ = (213,6 + 130,6) - (197,5 + 70,1) = 0,0766 кДж/моль.

3) DG⁰ = +2,80 - 298·0,0766 = -20,0 кДж.

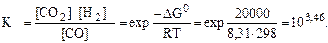
Концентрация Н₂О_(ж) принимается равной 1 и не включена в ЗДМ, т.к. это конденсированное состояние.

Пример 15. Реакция восстановления Fe₂O₃ водородом протекает по уравнению

Fe₂O_{3 (к)} + 3H₂ = 2Fe _(к) + 3Н₂О_(г); DH^о = + 96,61кДж.

Запишите закон действующих масс для этой реакции. Возможна ли эта реакция при стандартных условиях, если изменение энтропии DS⁰ = 0,1387 кДж/моль·К? При какой температуре начнется восстановление Fe₂O₃? Каково значение К при этой температуре?

Решение. Вычисляем DG⁰ реакции:

DG⁰ = DH⁰ - TDS⁰ = 96,61 - 298·0,1387 = 55,28 кДж.

ЗДМ для этой реакции c учетом агрегатного состояния веществ: .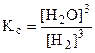

В то же время

=

=.

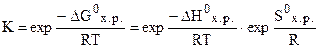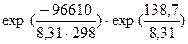
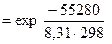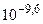Так как DG >0, то реакция при стандартных условиях невозможна; наоборот, при этих условиях идет обратная реакция окисления железа (коррозия). Найдем температуру, при которой DG = 0. При этом DH⁰ = TDS⁰, отсюда

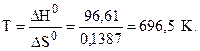
Следовательно, при температуре примерно 696,5 К начнется реакция восстановления Fe₂O₃. (“Примерно” потому, что при решении задачи мы не учитываем слабую зависимость DН и DS от температуры, а также то обстоятельство, что условие К < 1 означает не полное отсутствие реакции, а лишь малую степень её протекания). Иногда эту температуру называют температурой начала реакции. Подставляя в выражение для К значение Т = 696,5 К, убеждаемся, что К = 1.

Это значит, что за температуру начала реакции принята температура, при которой [H₂O] = [H₂].

Пример 16. Константа равновесия системы H₂ + I₂ 2HI при некоторой температуре равна 40. Определить, какая часть водорода и иода (%) перейдет в HI, если исходные концентрации этих веществ одинаковы и составляют 0,01 моль/л, а [HI]_исх = 0.

Решение. При решении подобных задач используется стехиометрическое уравнение реакции. Обозначим через x расход водорода к моменту наступления равновесия. Следовательно, равновесная концентрация Н₂ составит [H₂]_p =
(0,01 - x). Так как I₂ расходуется столько же, сколько и H₂ (по уравнению на 1 моль H₂ расходуется 1 моль I₂), то [I₂]_p = (0,01 - x). Из уравнения видно, что к моменту равновесия HI получается в 2 раза больше, чем расходуется H₂ , следовательно,
[HI]_p = 2x. Запишем выражение для константы равновесия и подставим числовые значения равновесных концентраций:

.

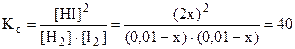Уравнение имеет два корня: х₁ = 0,0146, х₂ = 0,0076. Из двух значений х следует выбрать то, которое отвечает условию задачи. Исходные концентрации Н₂ и I₂ равны 0,01 моль/л. Следовательно, х не может иметь значение больше 0,01 и решение имеет одно значение -0,0076 моль/л. Таким образом, из 0,01 моль Н₂ и I₂ прореагировало 0,0076 моль, что составляет 76 %.

Пример 17. В системе CO + Cl₂ COCl₂ равновесные концентрации веществ составляют [CO₂]_p = 0,3; [CO]_p = 0,2; [COCl₂]_p = 1,2 моль/л. Вычислить константу равновесия системы и исходные концентрации CO и Cl₂.

Решение. Найдем константу равновесия, подставив числовые значения равновесных концентраций в выражение константы равновесия:

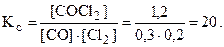
Исходная концентрация реагента равна сумме равновесной и израсходованной к моменту равновесия. Из уравнения реакции видно, что для образования 1 моль COCl₂ расходуется по 1 моль СО и Cl₂. Следовательно,

[CO]исх = [CO]_p + [CO]_изр = 0,2 + 1,2 = 1,4 моль/л.

[Cl₂]исх = [Cl₂]_p + [Cl₂]_изр = 0,3 + 1,2 = 1,5 моль/л.