1 По данным таблицы 1 вычислить дисперсию и среднее квадратическое отклонение.
Таблица 1 – Число продовольственных магазинов: выборка из 30 населенных пунктов Северной Франции.
| 4 7 69 20 3 8 30 234 14 5 | 4 4 4 1 1 6 4 3 1 1 | 5 405 2 18 2 2 16 3 696 10 |
2 Известны показатели изменения температуры почвы в течение месяца (в градусах Цельсия): -20; -15; -14; -11; -5; -4; - 3; - 1; +1; +5; +6; + 7. Определить коэффициент вариации.
3 Известны показатели изменения температуры почвы в течение месяца (в градусах Цельсия) на разных участках (таблица 2). Определить коэффициент вариации.
Таблица 2 – Показатели изменения температуры почвы в течение месяца
| № | Вариант задания | |||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | -20 -15 -14 -11 -5 -4 - 3 - 1 +1 +5 +6 + 7 | +10 +12 +11 +13 +4 +16 +12 +14 +13 +12 +14 +17 +13 +12 | -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 -1 0 +1 | +20 +17 +15 +13 +12 +10 +8 +8 +6 +5 +3 +2 +1 0 | -5 -4 -3 -2 -1 0 +1 +2 +3 +4 +5 +6 +7 +8 | -12 -13 -14 -15 -16 -15 -14 -13 -12 | -1 -1 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +10 +11 | -7 -6 -5 -3 -1 +1 +3 +3 +4 +5 +5 +6 +8 +8 | +2 +1 +2 +3 +6 +6 +7 +7 +3 +1 +5 +4 +4 +6 | -23 -20 -18 -12 -11 -7 -8 -5 -3 -1 0 +1 +2 +3 |
4 По данным вычислить: дисперсию; среднее квадратическое отклонение; ошибку среднего квадратического отклонения и точность данных
Таблица 3 - Содержание белка в суточном рационе питания (в расчете на душу населения)
| Страна | г/сут. |
| 1 | 2 |
| Австрия Бельгия Дания Финляндия Франция Германия Греция Ирландия Нидерланды Норвегия Португалия Испания Швеция Швейцария Великобритания Канада США Шри-Ланка Китай Индия Пакистан Израиль | 86,6 85,0 92,3 92,9 98,6 97,7 94,2 90,2 78,2 80,8 74,2 79,9 83,5 8,2 89,3 91,1 90,6 41,8 58,8 49,7 47,8 85,2 |
Вопросы для самоконтроля
1 Для чего используют показатели разнообразия признаков?
2 Какие показатели разнообразия признаков вы знаете?
3 Какие показатели используют как составляющие параметры нормального распределения?
4 Что показывает среднее квадратическое отклонение?
5 На что указывает дисперсия?
6 Что представляет собой коэффициент вариации?
7 Каким бывает разброс вариант в зависимости от значения коэффициента вариации?
Тема 4 Методы, используемые для установления
Подобия и отличия объектов и систем
Критерий Стъюдента (t)
Критерий наименьшей существенной разности (НСР)
Критерий Фишера (F)
4 Критерий соответствия (χ2)
Достоверность различий между генеральными совокупностями (Ni, N2...) может быть определена с помощью следующих критериев достоверности: критерия Стьюдента (t), наименьшей существенной разности (НСР), критерия соответствия (χ2), критерия Фишера (F).
1Критерий Стьюдента. Сравнение выборочных совокупностей по критерию Стьюдента t позволяет утверждать с некоторой долей уверенности сходство или различие между средними выборок по разнице между ними с использованием формулы
 (4.1)
(4.1)
где d – разность между средними (М1 – М2); тd – ошибка разности средних.
Выделяют три типа сравниваемых статистических совокупностей: независимые с одинаковым объемом выборок (N1 = N2), независимые с разным объемом выборок (N1  N2), сопряженные только с одинаковым объемом выборок (N1=N2).
N2), сопряженные только с одинаковым объемом выборок (N1=N2).
Независимые статистические совокупности могут быть получены на одной или нескольких точках, но при одинаковых условиях проведения эксперимента: например, измерение температуры воздуха в июле в г. Минске в течение нескольких лет и установление достоверных различий между этими показателями по годам исследований; определение содержания бора в автономных ландшафтах. Поэтому при установлении степени свободы в каждом независимом эксперименте выборочные совокупности суммируются.
Сопряженные статистические совокупности, как и независимые, однозначны по смыслу, их получают при проведении исследований на одном или нескольких ключах, но в разных условиях. Например: измерение температур воздуха и почвы на глубине 5 см в г. Минске в июле и сравнение полученных показателей (условия разные, точка наблюдения одна и та же); Степень свободы в каждом рассматриваемом эксперименте определяется по числу пар сравниваемых выборок (Nu). Рассмотрим расчеты достоверности различий для одинакового и разного объемов выборок.
Пример 1. При исследовании глубины расчленения рельефа в Воложинском районе N1 и Браславском районе N2 необходимо установить, объединять рассматриваемые участки в один геоморфологический район по степени расчленения рельефа или различать их как самостоятельные. Воложинский район – 20, 17, 16, 15, 15; Браславский район – 17,16, 15, 14, 14. (N1 = N2)
1) Находим среднее арифметическое для каждой выборки


Таблица 2 – Форма обработки вариант в независимых совокупностях
| х1 | (x1 – M1) | (x1 – M1)2 | х2 | (x2 – M2) | (x2 – M2)2 |
| 20 | 3,4 | 11,56 | 17 | 1,8 | 3,24 |
| 17 | 0,4 | 0,16 | 16 | 0,8 | 0,64 |
| 16 | - 0,6 | 0,36 | 15 | - 0,2 | 0,04 |
| 15 | - 1,6 | 2,56 | 14 | - 1,2 | 1,44 |
| 15 | - 1,6 | 2,56 | 14 | - 1,2 | 1,44 |
| Σ = 17,2 | Σ = 6,8 |
2) Находим разность между средними
d=М1 – M2 (4.2)
d = 16,6 – 15,2 = 1,4 м
При расчете разницы между средними из большей величины вычитают меньшую независимо от нумерации выборочных совокупностей.
3) Затем находят ошибки средних для каждой выборки в отдельности по формуле
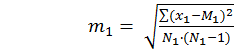
 (4.3)
(4.3)

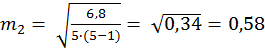
4) Находим ошибку разности между средними по формуле:
 (4.4)
(4.4)

5) Число степеней свободы устанавливают следующим образом:
v =N1 + N2 – 2 (4.5)
v= 5 + 5 – 2 = 8
6) Определяем Критерий Стьюдента
 (4.6)
(4.6)

Сопоставляем табличные значения критерия Стьюдента tт=2,32 и 3,36 (см. приложение 4) при Р=0,95 и 0,99 для v=8 с расчетным. Поскольку tТ >tФ,, то разность между средними признается несущественной (недостоверной). Следовательно, при выделении геоморфологических районов по глубине расчленения рельефа рассматриваемые участки необходимо объединить в один геоморфологический район.
Пример 2. При исследовании глубины расчленения рельефа в Воложинском районе N1 и Браславском районе N2 необходимо установить, объединять рассматриваемые участки в один геоморфологический район по степени расчленения рельефа или различать их как самостоятельные. Воложинский район – 20, 17, 16, 15, 15; Браславский район – 17,16, 15, 14, 14, 16. (N1 ≠ N2)
1) Находим среднее арифметическое для каждой выборки

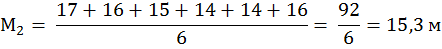
Таблица 2 – Форма обработки вариант в независимых совокупностях
| х1 | (x1 – M1) | (x1 – M1)2 | х2 | (x2 – M2) | (x2 – M2)2 |
| 20 | 3,4 | 11,56 | 17 | 1,7 | 2,89 |
| 17 | 0,4 | 0,16 | 16 | 0,7 | 0,49 |
| 16 | - 0,6 | 0,36 | 15 | - 0,3 | 0,09 |
| 15 | - 1,6 | 2,56 | 14 | - 1,3 | 1,69 |
| 15 | - 1,6 | 2,56 | 14 | - 1,3 | 1,69 |
| 16 | 0,7 | 0,49 | |||
| Σ = 17,2 | Σ = 7,34 |
2) Находим разность между средними d=М1 – M2 = 16,6 – 15,3 = 1,3 м
3) Ошибка разности средних, определяется по формуле
 (4.7)
(4.7)
где Σ(x1 – M1)2 – сумма квадратов отклонений от среднего для первой выборки; Σ (х2 –М2)2 – второй выборки; N1, N2– количество вариант в первой и второй выборках соответственно;

4) Число степеней свободы для разного объема выборок устанавливают следующим образом:
 (4.8)
(4.8)
 (4.9)
(4.9)
m1, m2— ошибка среднего первой и второй выборок соответственно
 (4.10)
(4.10)




5) Определяем Критерий Стьюдента
 (4.11)
(4.11)

Сопоставляем табличные значения критерия Стьюдента tт=2,45 и 3,71 (приложение 4) при Р=0,95 и 0,99 для v=6 с расчетным. Поскольку tТ > tФ,, то разность между средними признается несущественной (недостоверной)  рассматриваемые участки необходимо объединить в один геоморфологический район.
рассматриваемые участки необходимо объединить в один геоморфологический район.
Пример 3. Получены сопряженные выборки только с одинаковым объемом конечно-моренного ландшафта N1 и донно-моренного ландшафта N2. Число пар NП = 5. Воложинский район – 20, 17, 16, 15, 15; Браславский район – 17,16, 15, 14, 14 ( N1=N2).
1) Находим среднее арифметическое для каждой выборки


Таблица 3 – Форма обработки данных сопряженных наблюдений
| Глубина расчленения, м | di |
|
|
| |
| N1 | N2 | ||||
| 20 | 17 | 3 | 9 | + 1,6 | 2,56 |
| 17 | 16 | 1 | 1 | —0,4 | 0,16 |
| 16 | 15 | 1 | 1 | —0,4 | 0,16 |
| 15 | 14 | 1 | 1 | —0,4 | 0,16 |
| 15 | 14 | 1 | 1 | —0,4 | 0,16 |
| Σ=83 | Σ=76 | Σ=7 | Σ=13 | Σ=0 | Σ=3,20 |
| M1=16,6 | М2=15,2 |  = l,4 = l,4
|
| ||
2) Находим разность между средними
 (4.12)
(4.12)
 = 16,6 –15,2=1,4
= 16,6 –15,2=1,4
3) Находим ошибку разности между средними по формуле:
 (4.13)
(4.13)
 (4.14)
(4.14)
где di – разность между индивидуальными сопряженными вариантами в выборках;  – разность между средними сопряженных выборок; NП – число сопряженных пар в сопряженных выборках.
– разность между средними сопряженных выборок; NП – число сопряженных пар в сопряженных выборках.

4) Число степеней свободы устанавливают следующим образом:
v = NП – 2 (4.15)
v= 5 – 2=3
5) Определяем Критерий Стьюдента

Сопоставляем табличные значения критерия Стьюдента tт=3,18 и 5,84 (приложение 4) при Р=0,95 и 0,99 для v=3 с расчетным. Поскольку tФ > tТ при Р=0,95,то разность между средними признается существенной (достоверной). Следовательно, при выделении геоморфологических районов по глубине расчленения рельефа рассматриваемые участки необходимо рассматривать как самостоятельные.
2 Критерий наименьшей существенной разности (НСР) показывает то минимальное различие между средними, начиная с которого при выбранном уровне вероятности средние сравниваемые показатели существенно отличаются друг от друга. Величина критерия НСР выражается в тех же единицах, что и сравниваемые средние выборочных совокупностей, и определяется по формуле:
 (4.16)
(4.16)
где тd – ошибка разности средних; tT – табличное значение критерия Стьюдента при выбранном значении уровня вероятности.
Если разность между сравниваемыми средними в условиях эксперимента больше или равна величине НСР при Р = 0,95 или 0,99, то различие существенно. Если разность между средними меньше НСР, то различие обусловлено случайными факторами и признается недостоверным.
Проверим достоверность разности между средними арифметическими с использованием критерия НСР для случаев независимого и сопряженного наблюдений по формуле:
НСР0,95 = 2,32 • 1,1 = 2,55 м, НСР0,99 = 3,36• 1,1 = 3,696 м для независимых наблюдений;
НСР0,95 = 3,18 • 0,40= 1,27 м, НСР0,99 = 5,84 •,40 = 2,34 м для сопряженных наблюдений.
По величине НСР достоверное различие между средними установлено лишь при сопряженном наблюдении для уровня вероятности 0,95 (HCP0,95=1,27<  = 1,4 м).
= 1,4 м).
3 Критерий Фишера (F) используется для установления достоверностиразличия между совокупностями по дисперсиям. В таких случаях лучше использовать критерий Фишера F (положительное асимметричное распределение). Расчет критерия Фишера производится по формуле:
 (4.17)
(4.17)
где  по абсолютной величине должна быть больше, чем
по абсолютной величине должна быть больше, чем  .
.
Если величина расчетного критерия Фишера FФ не превышает величины приведенного в таблице FT (приложение 5), то различие между сравниваемыми дисперсиями считается недостоверным. При Fф > Fт эти дисперсии достоверно различны, а различие сравниваемых генеральных совокупностей признается неодинаковым. Степень свободы рассчитывается для сравниваемых совокупностей отдельно по формуле v = N – 1.
Пример. Необходимо установить достоверность различия в содержании гумуса в дерново-подзолистой заболоченной суглинистой почве для северной n1 и центральной n2 провинций РБ. Количество вариант в обеих совокупностях одинаковое.
В результате обработки данных получены следующие средние и дисперсии: M1 = 3,53 %,  =0,0024 %; M2 = 3,32 %,
=0,0024 %; M2 = 3,32 %,  =0,00032 %. Сравниваемые совокупности весьма сходны и можно констатировать отсутствие различия между ними. Однако пределы колебаний в совокупностях существенно отличаются по вариантам (более чем в 2 раза), что требует для доказательства сходства или различия использовать критерий Фишера. В результате вычислительных операций получены следующие результаты:
=0,00032 %. Сравниваемые совокупности весьма сходны и можно констатировать отсутствие различия между ними. Однако пределы колебаний в совокупностях существенно отличаются по вариантам (более чем в 2 раза), что требует для доказательства сходства или различия использовать критерий Фишера. В результате вычислительных операций получены следующие результаты:
Fф =  /
/ 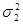 = 0,0024: 0,00032 = 7,5.
= 0,0024: 0,00032 = 7,5.
Степень свободы равна: v1 = 5—1=4,
v2 = 5—1=4.
Для P=0,95 и 0,99 FT = 6,39 и 15,98 (приложение 5) соответственно. Поскольку Fф>Fт, то различие в содержании гумуса по провинциям признается существенным при уровне вероятности Р=0,95.
4 Критерий соответствия (χ2) -количественное изучение явлений требует создания гипотез, с помощью которых можно объяснить эти явления. Для этой цели используется критерий кси-квадрат (χ2), или критерий соответствия, который рассчитывается по формуле
 (4.18)
(4.18)
где φ, φ' – число наблюдений в опыте фактическое и теоретически ожидаемое.
Если расчетные значения кси-квадрат превышают табличные (приложение 6), то гипотеза о независимости признаков отвергается. Если  <
< 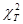 , то признаки можно считать независимыми.
, то признаки можно считать независимыми.
Степень свободы при проверке гипотезы о нормальном распределении вычисляется по формуле
v = k –3 (4.19)
где k – число классов.
Достоверность расчетных данных можно также оценить по формуле:
 (4.20)
(4.20)
Различие считается достоверным, если D  3. При обработке данных по условиям применения критерия кси-квадрат требуется, чтобы частота в каждом классе была не менее пяти.
3. При обработке данных по условиям применения критерия кси-квадрат требуется, чтобы частота в каждом классе была не менее пяти.
Пример. Следует определить число сельских жителей с бронхолегочными заболеваниями, обострение болезни у которых связано с природными условиями местожительства.
Для обработки выборочных вариант составляем таблицу. Всего выявлен 71 больной житель из 639 обследованных одного возраста и пола по 9 человек в каждом населенном пункте.
Таблица 4 - Сравнение эмпирических и теоретических частот с использованием критерия кси-квадрат
| Число обследованных жителей (классы) | Число фактических больных, φ | Число теоретически больных, φ' | φ – φ' | (φ- φ')2 | (φ- φ')2 φ' |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1-71 72-142 143-213 214-284 285-355 356-426 427-497 498-568 569-639 |  10
15
12
10
10
15
12
10

|  13
14
10
11
13
14
10
11
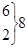
| -4 (11-15) -3 1 2 -1 5 | 16 9 1 4 1 25 | 1,06 0,69 0,07 0,40 0,09 3,12 |
| i=9 | N=71 | N=71 |
| ||
Для обработки данных количество обследованных сгруппировано в 9 классов. Поскольку частота в каждом классе φ, φ' должна быть не менее 5, объединяем первые три и последние два класса в столбцах 2 и 3. Получаем новые классы с частотами 11,15 и 13,8 (всего по 6 классов распределения). Затем производим расчеты, которые позволяют получить критерий 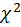 (см. таблицу).
(см. таблицу).
Сравниваем  и
и  при величине степени свободы v= k –3=6–3=3 и для Р= 0,95. Поскольку
при величине степени свободы v= k –3=6–3=3 и для Р= 0,95. Поскольку  =5,43<
=5,43<  =7,815 (приложение 6), теоретическое распределение частот несущественно отличается от эмпирического, а гипотеза признается состоятельной.
=7,815 (приложение 6), теоретическое распределение частот несущественно отличается от эмпирического, а гипотеза признается состоятельной.
Определим также достоверность 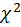 :
:

Полученная величина D=0,99<3, следовательно, рассчитанное значение 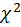 показывает достоверное влияние природных условий на распространение бронхолегочных заболеваний.
показывает достоверное влияние природных условий на распространение бронхолегочных заболеваний.
 2020-05-25
2020-05-25 262
262




 =1,4
=1,4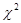 =5,43
=5,43






