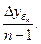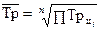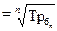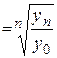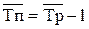В основе расчёта показателей ряда динамики лежит сравнительный анализ уровней ряда либо с постоянной, либо с переменной базой сравнения. При постоянной базе сравнения каждый уровень ряда сравнивается с одним и тем же показателем (уровнем), принятым за базу сравнения (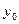 ). Как правило, в качестве базисного уровня выбирается начальный уровень динамического ряда или уровень, с которого начинается качественно новый этап развития явления. При переменной базе сравнения каждый уровень ряда сравнивают с непосредственно ем предшествующим (
). Как правило, в качестве базисного уровня выбирается начальный уровень динамического ряда или уровень, с которого начинается качественно новый этап развития явления. При переменной базе сравнения каждый уровень ряда сравнивают с непосредственно ем предшествующим (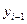 ).
).
Показатели динамики с постоянной базой сравнения называются базисными, а показатели с переменной базой сравнения – цепными.
1). Абсолютный прирост – это разность между двумя уровнями ряда динамики в исходных единицах измерения:
- базисный: 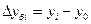
- цепной: 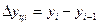
Он показывает, на сколько данный уровень ряда превышает уровень, принятый за базу сравнения.
По знаку абсолютного изменения делается вывод о характере развития явления: при 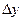 > 0 – рост,при
> 0 – рост,при 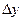 < 0 – спад,при
< 0 – спад,при 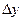 = 0 – стабильность.Абсолютный прирост может иметь отрицательное значение, если уровень изучаемого периода ниже уровня базисного периода или предшествующего. Цепной абсолютный прирост называют скоростью роста.
= 0 – стабильность.Абсолютный прирост может иметь отрицательное значение, если уровень изучаемого периода ниже уровня базисного периода или предшествующего. Цепной абсолютный прирост называют скоростью роста.
Между цепным и базисным абсолютным приростом существует взаимосвязь: сумма цепных абсолютных приростов равна абсолютному приросту последнего уровня ряда динамики: 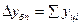
2). Темп роста – это отношение двух сравниваемых уровней ряда, может выражаться в виде коэффициента, но чаще в %.
Цепной: 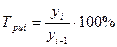
Базисный: 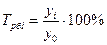
Он показывает, во сколько раз данный уровень ряда превышает уровень базисного периода. Если темп роста > 100%, то идёт увеличение изучаемого уровня по сравнению с базисным или предыдущим, и наоборот.
Между базисным и цепными темпами роста существует взаимосвязь – произведение последовательных цепных темпов роста равно базисному темпу роста последнего уровня ряда динамики:
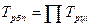
Частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста:
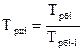 .
.
3). Темп прироста характеризует абсолютный прирост в относительных величинах. Определяется двумя способами:
а) как отношение абсолютного прироста к уровню, принятому за базу сравнения:
Базисный: 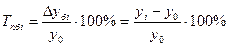
Цепной: 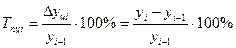
б) как разность между темпом роста и 100%:
Базисный: 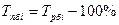
Цепной: 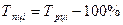
Если уровни ряда динамики сокращаются, то соответствующие показатели темпов прироста будут с минусом, так как они характеризуют уменьшение ряда динамики в процентах.
4). Темп наращивания показывает рост во времени экономического потенциала. Вычисляется делением цепных абсолютных приростов на уровень, принятый за постоянную базу сравнения:
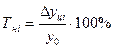
5). Абсолютное значение одного процента прироста определяется через отношение цепного абсолютного прироста к цепному темпу прироста за соответствующий период:
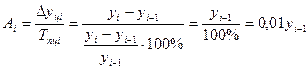 .
.
Он показывает, что замедление темпов прироста не всегда сопровождается уменьшением абсолютных приростов.
6). Относительное ускорение представляет собой разность следующих друг за другом темпов роста (прироста) в одном ряду или темпов роста (прироста) за один период в двух смежных рядах динамики:
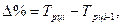
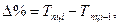
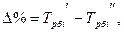
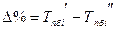
Относительное ускорение выражается в процентных пунктах роста. В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно складывать, в результате чего получается темп прироста соответствующего периода по сравнению с базисным уровнем.
7). Коэффициент опережения определяется как отношение последующего темпа роста (прироста) к предыдущему или через соотношение темпов роста или темпов прироста за одинаковые периоды времени по двум динамическим рядам:
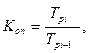
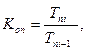
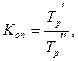
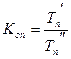
С помощью коэффициентов опережения сравнивают динамические ряды одинакового содержания, но относящиеся к разным территориям (странам, регионам, районам) или к различным организациям (министерствам, предприятиям), а также ряды разного содержания, характеризующие один и тот же объект (рост потребительских цен и рост среднемесячной зарплаты за одни и те же периоды времени).
Средние показатели
1). Средний уровень ряда динамики – это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности, он характеризует типическую величину абсолютных уровней ряда и зависит от вида ряда динамики:
а) для интервального ряда абсолютных величин с равными периодами (интервалами времени) используется средняя арифметическая простая:
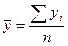
б) для моментного ряда с равными интервалами между датами применяется средняя хронологическая:
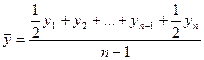
в) для моментного ряда с неравными интервалами между датами рассчитывается средняя арифметическая взвешенная:
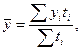
где 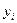 - уровни ряда, сохраняющиеся без изменения на протяжении интервала времени
- уровни ряда, сохраняющиеся без изменения на протяжении интервала времени 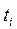 .
.
2). Средний абсолютный прирост рассчитывается как средняя арифметическая из показателей скорости роста за отдельные промежутки времени:
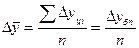 или
или 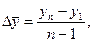
где n - число уровней ряда динамики;
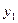 - первый уровень ряда динамики;
- первый уровень ряда динамики;
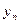 - последний уровень ряда динамики;
- последний уровень ряда динамики;
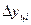 - цепные абсолютные приросты;
- цепные абсолютные приросты;
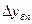 - последний базисный абсолютный прирост.
- последний базисный абсолютный прирост.
3). Средний коэффициент роста можно определить, пользуясь формулами:
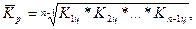
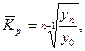
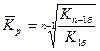
где n - число уровней ряда;
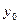 - уровень ряда, принятый за базу для сравнения;
- уровень ряда, принятый за базу для сравнения;
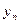 - последний уровень ряда;
- последний уровень ряда;
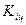 - цепные коэффициенты роста;
- цепные коэффициенты роста;
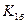 - первый базисный коэффициент роста;
- первый базисный коэффициент роста;
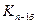 - последний базисный коэффициент роста.
- последний базисный коэффициент роста.
Средний коэффициент роста показывает, во сколько раз в среднем за отдельные составляющие рассматриваемого периода времени изменились уровни динамического ряда.
4). Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах:
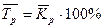
5). Средний темп прироста:
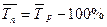
Таблица 2.1. Уровни (показатели) ряда динамики
| Показатель | Формула | |
| Базисные | Абсолютный прирост | Δ 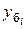 = yi – у 0 = yi – у 0 |
| Темп роста | 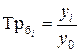 | |
| Темп прироста | 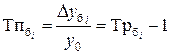 | |
| Цепные | Абсолютный прирост | Δ 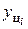 = yi – yi -1 = yi – yi -1 |
| Темп роста | 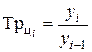 | |
| Темп прироста |
| |
| Темп наращивания |
| |
| Абсолютное значение 1% прироста |
| |
| Средние | Абсолютный прирост |
|
| Темп роста |
| |
| Темп прироста |
|
Пример 1.
Производственная мощность на предприятии характеризуется следующими данными:
Интервальный ряд динамики
| Показатель | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 |
| Производствен-ная мощность т/сутки | 206,4 | 208,3 | 210,2 | 211,5 | 213,4 | 217,3 |
Определить:
1. Все аналитические показатели ряда динамики.
2. Взаимосвязь цепных и базисных темпов роста.
3. Привести графическое изображение динамики производственной мощности.
Решение:
1). Абсолютный прирост
Цепные: 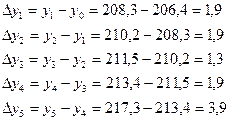
Базисные: 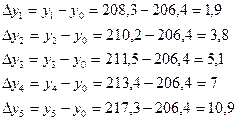
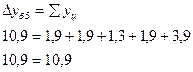
2). Темп роста
Базисные: 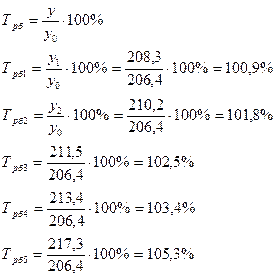
Цепные: 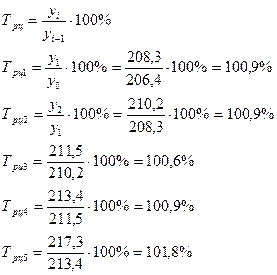
3). Темп прироста
Базисные: 1-й способ: 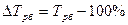
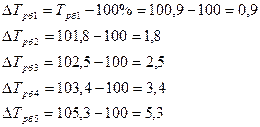
2-й способ: 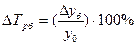
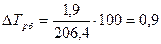 и т.д.
и т.д.
Цепные: 1-й способ: 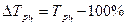
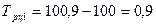
2-й способ: 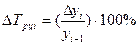
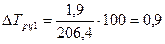
4). Темп наращивания: 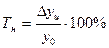
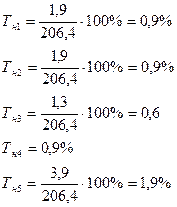
5). Средний абсолютный прирост: 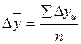
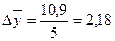
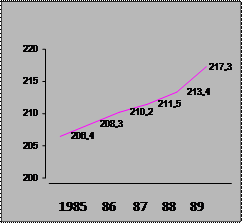 |
Рис. 1. Динамика производственной мощности
Пример 2.
Среднемесячные денежные доходы на душу населения по области составили (тыс. руб.):
| 2006 | 2007 | 2008 | 2009 | 2010 |
| 5,4 | 6,2 | 8,3 | 10,2 | 10,9 |
Определить цепные и базисные показатели динамического ряда.
Решение:
1). Абсолютные приросты:
а) базисные:
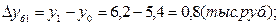
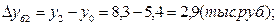
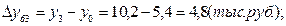
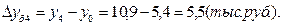
б) цепные:
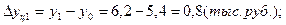
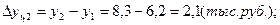
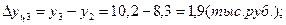
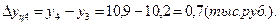
2). Темпы роста:
а) базисные:
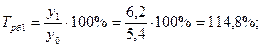
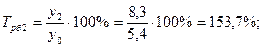
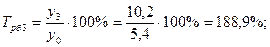
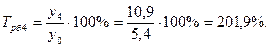
б) цепные:
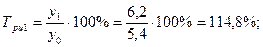
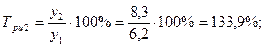
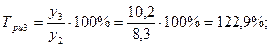
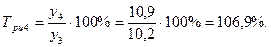
3). Темпы прироста:
а) базисные:
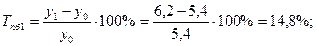
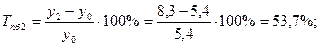
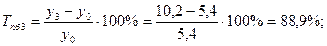
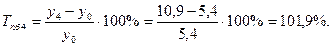
б) цепные:
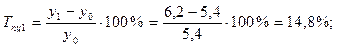
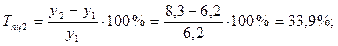
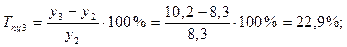
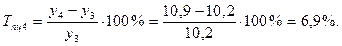
4). Абсолютное значение одного процента прироста:
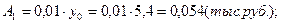
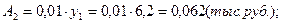
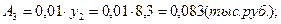
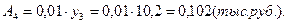
Пример 3.
Используя взаимосвязь показателей динамики, определить уровни ряда динамики и недостающие в таблице цепные показатели динамики по следующим данным:
| Год | Производство продукции, млн. руб. | По сравнению с предыдущим годом | |||
| Абсолютный прирост, млн. руб. | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, млн. руб. | ||
| 2008 | 92,5 | ||||
| 2009 | 4,8 | ||||
| 2010 | 104,0 | ||||
| 2011 | 5,8 | ||||
| 2012 | |||||
| 2013 | 7,0 | 1,15 | |||
Решение оформить в таблице.
Решение:
1). 2009 год:
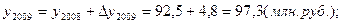
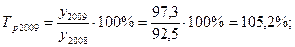
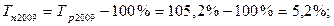
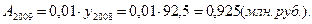
2). 2010 год:
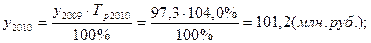
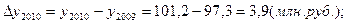
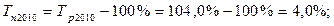
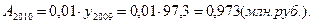
3). 2011 год:
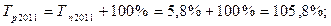
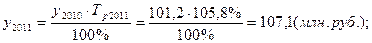
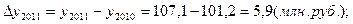
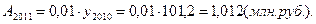
4). 2012 год:
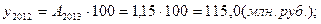
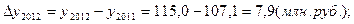
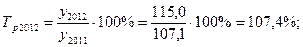
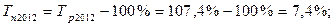
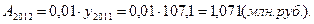
5). 2013 год:
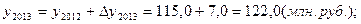
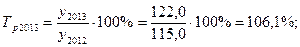
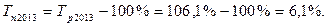
Исходная таблица приобретает вид:
| Год | Производство продукции, млн. руб. | По сравнению с предыдущим годом | |||
| Абсолютный прирост, млн. руб. | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, млн. руб. | ||
| 2008 | 92,5 | ||||
| 2009 | 97,3 | 4,8 | 105,2 | 5,2 | 0,925 |
| 2010 | 101,2 | 3,9 | 104,0 | 4,0 | 0,973 |
| 2011 | 107,1 | 5,9 | 105,8 | 5,8 | 1,012 |
| 2012 | 115,0 | 7,9 | 107,4 | 7,4 | 1,071 |
| 2013 | 122,0 | 7,0 | 106,1 | 6,1 | 1,150 |
Пример 4.
Имеются данные об остатках вкладов физических лиц в отделении банка, тыс. руб.:
- на 1 января – 1400;
- на 1 апреля – 1420;
- на 1 июля – 1428;
- на 1 октября – 1522;
- на 1 января следующего года – 1526.
Определить:
1) средний остаток вкладов населения в каждом квартале;
2) средний годовой остаток вкладов населения.
Решение:
1). Средние остатки вкладов населения по кварталам:
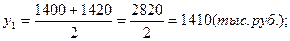
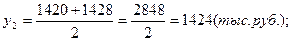
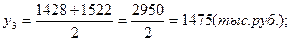
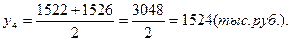
2). Среднегодовой остаток вкладов населения для моментного ряда с равными интервалами определяется по формуле средней хронологической:
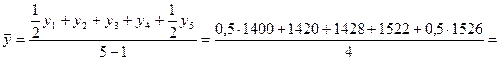
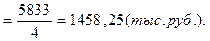
Пример 5.
Списочная численность работников организации в прошлом году составила: на 1 января – 530 чел., на 1 марта – 570 чел., на 1 июня – 520 чел., на 1 сентября – 430 чел., а на 1 января текущего года – 550 чел. Вычислить среднегодовую численность работников организации за минувший год.
Решение:
По условиям задачи имеется моментный ряд динамики с неравными интервалами времени: t1 =2 месяца, t2 =3 месяца, t3 =3 месяца, t4 =4 месяца.
Среднесписочные численности работников за каждый из этих периодов:
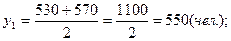
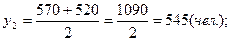
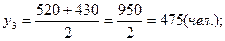
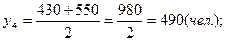
Среднегодовое значение численности работников необходимо рассчитывать по формуле средней арифметической взвешенной:
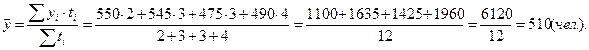
 2020-05-25
2020-05-25 10290
10290
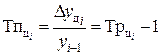
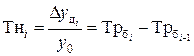
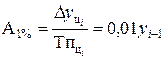
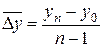 =
=