2020-05-25
121
Фильтр Калмана представляет собой математический аппарат, позволяющий проводить фильтрацию данных, поступающих в реальном времени, не накапливая их для анализа [10]. Данный метод проводит предсказание поведения сигнала s (t) по имеющимся наблюдениям y (t), содержащим ошибку v (t) таким образом, что y (t) = s (t) + v (t), где t – номер отсчёта по временной координате. Процесс называется фильтрацией в силу того, что получаемые данные содержат в себе шумы, от которых необходимо избавиться для получения наилучшей оценки исходного сигнала s (t) [11].
Касаемо модели сигнала, описанной в уравнении (1), важно отметить, что косинус является нелинейной функцией[НБ4], поэтому классический линейный фильтр Калмана также неприменим для данной модели сигнала. При известной априорной модели нелинейного сигнала удобно использовать нелинейный (расширенный) фильтр Калмана, но помимо него существуют и другие методы для обработки таких сигналов, например, последовательный метод Монте-Карло (ПММК). Однако сравнение времени выполнения двух данных методов в системе ОКТ показало, что расширенный фильтр Калмана работает быстрее вне зависимости от размера входных данных [12]. Преимущество ПММК перед фильтром Калмана состоит в том, что он более адаптивен к изменению входных данных и при использовании в ОКТ не теряется качество выходных изображений, но в рамках данной работы более приоритетны скорость и вычислительная сложность алгоритма. Исходя из перечисленных выше факторов, расширенный фильтр Калмана был выбран для исследования в этой работе.
Фильтр Калмана основан на дискретизированных по времени линейных динамических системах. Такие системы можно смоделировать с помощью Марковских цепей при помощи линейных операторов и слагаемых с нормальным распределением [13]. Состояние системы описывается вектором конечной размерности — вектором состояния. В каждый такт времени линейный оператор действует на вектор состояния и переводит его в другой вектор состояния, добавляется некоторый вектор нормального шума и в общем случае вектор управления, моделирующий воздействие системы управления [14]. Вектор состояния содержит в себе компоненты интерферометрического сигнала, модель которого описана в первой главе. Набор параметров в уравнении (1) можно преобразовать в вектор состояния, он будет выглядеть следующим образом:
, (3)
где 
– компонента оценки фоновой составляющей сигнала, 
– компонента оценки амплитуды, 
– компонента оценки фазы. Далее вводятся компоненты для оценивания всех необходимых составляющих сигнала: вектор компонентов 
из уравнения (2), содержащий 3 элемента, описанных выше – оценки компонент амплитуды, фона и фазы. При инициализации алгоритма данные компоненты оценок представляют собой вектора, размерность которых соответствует размерности исходного сигнала, а начальные значения данных компонент равны нулю.
На k -ом шаге работы алгоритма вектор состояния рассчитывается по следующей формуле:
(4)
где 
– предсказанное значение, определяемое как 
= f (
[НБ5] 
– значение исходного сигнала на k-ом шаге; 
– матричный коэффициент усиления фильтра, определяющий вклад невязки наблюдения и предсказания в оценку вектора параметров. Коэффициент усиления 
вычисляется следующим образом:
, (5)
где 
– предсказание ковариационной матрицы ошибок,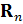 
– ковариационная матрица шума наблюдения, а 
– матрица первых производных функции h (θ) по компонентам исходного сигнала [15]. Рассчитанная матрица H представлена следующим образом:
. (6)
Компоненты предсказания ковариационной матрицы ошибок и ковариационной матрицы шума наблюдения, содержащиеся в уравнении (4), определяют вклад каждой оценки компоненты вектора параметров , то есть, какую из компонент вектора параметров фильтр обрабатывает в большей степени. Ковариационная матрица ошибок 
описана следующим образом:
= 
, (7)
где 
дисперсия оценки компоненты фона, 
– дисперсия оценки компоненты амплитуды, 
– дисперсия оценки компоненты фазы. Ковариационная матрица шума наблюдения 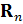представлена в виде матрицы единичной размерности.
