2020-05-25
388
| n\P | 0,5 | 0,7 | 0,9 | 0,95 | 0,98 | 0,999 |
| 2 | 1,00 | 2,00 | 6,30 | 12,7 | 31,8 | 636,6 |
| 3 | 0,82 | 1,3 | 2,90 | 4,30 | 7,0 | 31,6 |
| 4 | 0,77 | 1,25 | 2,4 | 3,2 | 4,5 | 12,9 |
| 5 | 0,74 | 1,2 | 2,1 | 2,8 | 3,7 | 8,6 |
| 6 | 0,73 | 1,15 | 2,0 | 2,6 | 3,4 | 6,9 |
| 7 | 0,72 | 1,1 | 1,9 | 2,4 | 3,1 | 6,0 |
| 8 | 0,71 | 1,1 | 1,9 | 2,4 | 3,0 | 5,4 |
| 9 | 0,71 | 1,1 | 1,9 | 2,3 | 2,9 | 5,0 |
| 10 | 0,70 | 1,1 | 1,8 | 2,3 | 2,8 | 4,8 |
| 20 | 0,69 | 1,1 | 1,7 | 2,1 | 2,5 | 3,9 |
| 60 | 0,68 | 1,0 | 1,7 | 2,0 | 2,4 | 3,5 |
| 0,67 | 1,0 | 1,6 | 2,0 | 2,3 | 3,3 |
Относительная ошибка определяется по Формуле
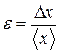(16)
Итак, алгоритм обработки результатов многократных измерений физической величины х следующий.
1. Провести n измерений и зафиксировать результаты единичных измерений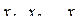 
.
2. По формуле (8) определить среднеарифметическое значение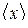 
величины х.
3. Вычислить отклонения единичных измерений от среднеарифметического значения по формуле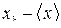 
4. Вычислить величины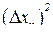 
, 
.
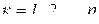5. Вычислить среднеквадратичную погрешность по формуле (7).
6. Задать надежность р (обычно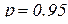 
) и определить из таблицы 1.1 коэффициент Стьюдента для n измерений.
|
|
|
7. Вычислить величину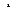 
по формуле (15).
8. Представить результат в стандартном виде с указанием его надежности:
, 
.
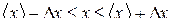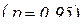9. Вычислить относительную ошибку по формуле (16).
