 Очень часто цель эксперимента заключается в том, чтобы из опыта найти неизвестный параметр в известной формуле. Так, например, пройденный путь при равноускоренном движении без начальной скорости описывается формулой
Очень часто цель эксперимента заключается в том, чтобы из опыта найти неизвестный параметр в известной формуле. Так, например, пройденный путь при равноускоренном движении без начальной скорости описывается формулой 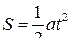 (известна зависимость S от t, требуется определить a); зависимость сопротивления чистого полупроводника от температуры вычисляется по формуле
(известна зависимость S от t, требуется определить a); зависимость сопротивления чистого полупроводника от температуры вычисляется по формуле 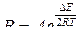 (известна зависимость R от Т, требуется определить ширину запрещённой зоны
(известна зависимость R от Т, требуется определить ширину запрещённой зоны 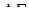 и параметр А). Обе приведенные зависимости являются нелинейными, но, если в первом случае строить график S от
и параметр А). Обе приведенные зависимости являются нелинейными, но, если в первом случае строить график S от 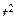 , а во втором ln R от
, а во втором ln R от 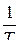 , то оба графика будут представлять из себя прямые линии. Тангенс угла наклона прямой к оси
, то оба графика будут представлять из себя прямые линии. Тангенс угла наклона прямой к оси 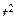 равен
равен 
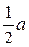 в первом случае и
в первом случае и 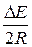 – во втором, вторая прямая пересекает ось ln R в точке ln A.
– во втором, вторая прямая пересекает ось ln R в точке ln A.
Однако, из-за наличия погрешностей измерения, а в некоторых случаях из-за статического характера исследуемых зависимостей экспериментальные точки не ложатся на теоретическую прямую(см. рисунок 1).
Возникает следующая задача: по экспериментальным точкам провести прямую наилучшим образом, т.е. проходящую по возможности ближе ко всем точкам. В случае числа экспериментальных точек 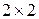 количественным критерием является сумма квадратов отклонений «теоретических»
количественным критерием является сумма квадратов отклонений «теоретических»  от «экспериментальных»
от «экспериментальных» 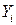 ; точек (квадраты берутся для того, чтобы избежать взаимной компенсации положительных и отрицательных отклонений). Метод, использующий этот критерий, носит название метода наименьших квадратов.
; точек (квадраты берутся для того, чтобы избежать взаимной компенсации положительных и отрицательных отклонений). Метод, использующий этот критерий, носит название метода наименьших квадратов.
Пусть имеется набор n экспериментальных точек 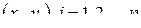
Теоретическая зависимость имеет вид:
 . (22)
. (22)
Тогда упомянутая сумма определяется выражением
 . (23)
. (23)
Коэффициенты 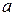 и
и 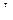 находятся из условия, чтобы
находятся из условия, чтобы  была минимальна. Необходимые условия минимума дают систему уравнений:
была минимальна. Необходимые условия минимума дают систему уравнений:
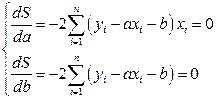 (24)
(24)
или
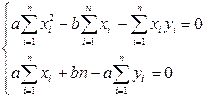 . (25)
. (25)
Решение системы (25) дает следующие формулы для определения 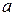 и
и  :
:
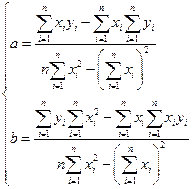 . (26)
. (26)
После того как коэффициенты a и b найдены, зависимость 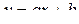 может быть использована как градуировочная для нахождения неизвестного значения
может быть использована как градуировочная для нахождения неизвестного значения 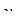 по графику в точке
по графику в точке 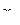 . Погрешность
. Погрешность 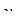 определяется как погрешность
определяется как погрешность 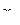 (если
(если 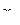 – экспериментальная величина) так и погрешностями проведения графика:
– экспериментальная величина) так и погрешностями проведения графика:
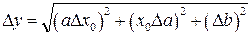 (27)
(27)
Здесь 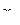 находится обычными методами, а погрешности
находится обычными методами, а погрешности 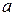 и
и 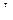 определяются следующими формулами:
определяются следующими формулами:
 , (28)
, (28)
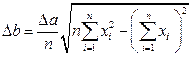 . (29)
. (29)
В заключение приведем формулу метода наименьших квадратов в случае более простой теоретической зависимости:
 (30)
(30)
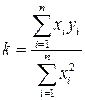 ,
, 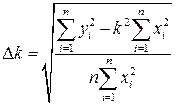 (31)
(31)
 2020-05-25
2020-05-25 126
126








