2020-05-25
160
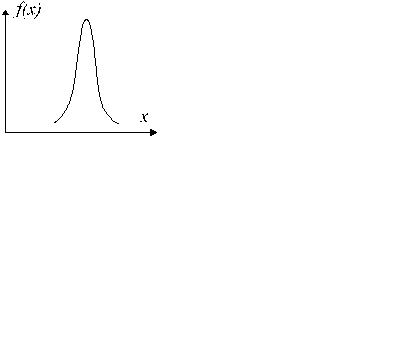
22. СЛУЧАЙНАЯ ВЕЛИЧИНА РАСПРЕДЕЛЕНА ПО НОРМАЛЬНОМУ ЗАКОНУ, ЕСЛИ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ ВЫРАЖАЕТСЯ ФОРМУЛОЙ..............(1). ГРАФИК НОРМАЛЬНОГО ЗАКОНА 
РАСПРЕДЕЛЕНИЯ ИМЕЕТ ВИД..............(2).
23. ГРАФИКИ НОРМАЛЬНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН, ДЛЯ КОТОРЫХ 
И 
, ИМЕЮТ ВИД..................(1).
24. ГРАФИКИ НОРМАЛЬНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН, ДЛЯ КОТОРЫХ 
и 
, ИМЕЮТ ВИД..................(1).
25. ГРАФИКИ НОРМАЛЬНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН, ДЛЯ КОТОРЫХ 
И 
, ИМЕЮТ ВИД.....................(1).
| Инструкция для студентов. Задания состоят в выборе правильных пар из двух множеств. Каждому элементу левого задающего множества L соответствует определенный элемент или два (смотрите эталон ответа) правого множества выбора R. |
СООТВЕТСТВИЕ МЕЖДУ СОБЫТИЯМИ И ЗАКОНАМИ
LR
ЗАКОНЫ СОБЫТИЯ
1. Р(А + В) = Р(А)+Р(В) А.Независимые.
2. Р(А +В) = Р(А)+Р(В)-Р(А) 
Р(В) Б.Зависимые.
3. Р(А • В) = Р(А) Р(В) В. Совместные.
4. Р(А • В) = Р(А) Р(B/A) Г. Несовместные
|
|
|
Эталон: 1 ___, 2___, 3___, ____,4___,____.
27. СООТВЕТСТВИЕ МЕЖДУ НАЗВАНИЕМ И ФОРМУЛОЙ
LR
НАЗВАНИЕ ФОРМУЛА
1. Статистическое определение вероятности А.Р =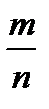 
2. Классическое определение вероятности Б. M (x) =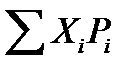 
3. Математическое ожидание В. Р =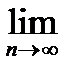 
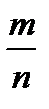4.Дисперсия. Г. 
.
Д. D(x)= M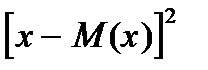 
Эталон: 1___, 2__, 3___, 4 ___.
СООТВЕТСТВИЕ МЕЖДУ СОБЫТИЯМИ И ВЕРОЯТНОСТЯМИ
LR
СОБЫТИЯ ВЕРОЯТНОСТИ
1. Равновозможные. А.Р (А)+ Р(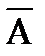
)=1
2. Невозможные. Б.P (A) = 1
3. Достоверные. В.P (A) = 0,8
4. Противоположные. Г. P (A) = 0
Д.P (A) = P(B)
Эталон: 1___, 2___, 3___, 4____.
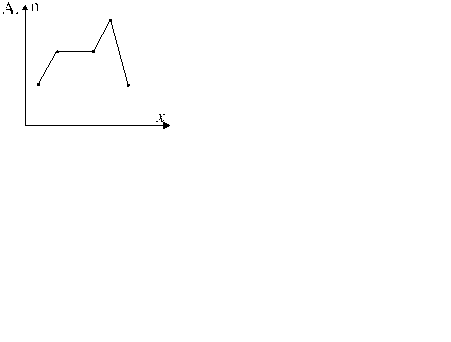
29. СООТВЕТСТВИЕ МЕЖДУ ФУНКЦИЯМИ И ГРАФИКАМИ
LR
НАЗВАНИЕ ГРАФИКИ
|
|
|
|
| Б |
1. Интегральная функция распре- деления для дискретной случайной величины.
2. Интегральная функция распре-
деления для непрерывной случай-
|
|
|
|
ной величины.
3. Дифференциальная функция
распределения.
Эталон: 1___, 2___, 3___.
