2020-05-21
129
Для правой половины рассматриваемого отрезка разности лучше вычислять справа налево. В этом случае:
t=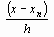 
,
o. е. t 0 и интерполяционную формулу Ньютона можно получить в виде:
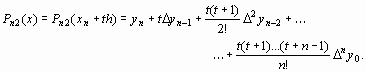
| (16) |
Формулу (16) называют второй интерполяционной формулой Ньютона для интерполирования назад.
Пример 3. Дана таблица значений y = lg x семизначных логарифмов
| х | у |
| 1000 | 3,0000000 |
| 1010 | 3,0043214 |
| 1020 | 3,0086002 |
| 1030 | 3,0128372 |
| 1040 | 3,0170333 |
| 1050 | 3,0211893 |
Найти lg 1044.
Составляем таблицу разностей (Таблица 1).
Таблица 1.
Таблица разностей функции у = lg x
Примем xn = 1050,
тогда
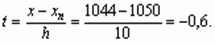
Используя подчеркнутые разности, в силу формулы (16) будем иметь:
lg 1044 = 3,0211893 + (-0,6) 0,0041560 +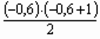 
0,0000401 + 
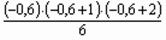0,0000008 = 3,0187005.
Как первая, так и вторая интерполяционные формулы Ньютона могут быть использованы для экстраполирования функции, т. е. для нахождения значений функции y для значений аргументов х, лежащих вне пределов таблицы. Если х < х 0 и х близко к х 0, то выгодно применять первую интерполяционную формулу Ньютона, причем тогда
|
|
|
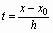< 0.
Если х < хn и х близко к хn, то удобнее пользоваться второй интерполяционной формулой Ньютона, причем
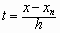> 0.
Таким образом, первая интерполяционная формула Ньютона обычно используется для интерполирования вперед и экстраполирования назад, а вторая интерполяционная формула Ньютона, наоборот - для интерполирования назад и экстраполирования вперед.
Операция экстраполирования менее точна, чем операция интерполяции в узком смысле слова.
