2020-05-21
240
Постановка задачи. Найти решение ОДУ первого порядка
на отрезке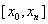 
при условии 
При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом 
, расчетными узлами служат точки 
промежутка [ x 0, xn ].
Целью является построение таблицы
| xi | x 0 | x 1 | … | xn |
| yi | y 0 | y 1 | … | yn |
т.е. ищутся приближенные значения y в узлах сетки.
Интегрируя уравнение на отрезке 
, получим
Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка
,
то получим явную формулу Эйлера:
, 
.
Порядок расчетов:
Зная 
, находим 
, затем 
т.д.
Геометрическая интерпретация метода Эйлера:
Пользуясь тем, что в точке x0 известно решение y (x 0) = y 0 и значение его производной 
, можно записать уравнение касательной к графику искомой функции 
в точке 
: 
. При достаточно малом шаге h ордината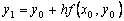 
этой касательной, полученная подстановкой в правую часть значения 
, должна мало отличаться от ординаты y (x 1) решения y (x) задачи Коши. Следовательно, точка 
пересечения касательной с прямой x = x 1 может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую 
, которая приближенно отражает поведение касательной к в точке 
. Подставляя сюда 
(т.е. пересечение с прямой x = x 2), получим приближенное значение y (x) в точке x 2: 
и т.д. В итоге для i –й точки получим формулу Эйлера.
Явный метод Эйлера имеет первый порядок точности или аппроксимации.
Если использовать формулу правых прямоугольников: 
, то придем к методу
, .
Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения 
по известному значению 
требуется решать уравнение, в общем случае нелинейное.
Неявный метод Эйлера имеет первый порядок точности или аппроксимации.
Рассмотрим несколько численных методов решения дифференциальных уравнений первого порядка. Описание численных методов приводится для уравнения в виде у'=f(x,y).
1. Метод Эйлера.
Рассмотрим два варианта вывода расчетных формул
· вариант 1 (аналитический) у=f (x,y)
| y1=y0+h*f(x0,y0) x1=x0+h | Расчетные формулы для 1-го шага |
| yi+1=yi+h*f(xi,yi) xi+1=xi*h | Расчетные формулы для i-го шага |
· вариант 2 (графический)
| 
y1=y0+f(x0,y0)*h;
x1=x0+h
yi+1=yi+h*f(xi,yi)
|
| k1=h*f(xi,yi) yi+1=yi+ki xi+1=xi+h | Аналогично варианту 1 |
Пример. Решить задачу Коши:
.
Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта.
Точное решение: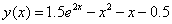 
Расчетные формулы по явному методу Эйлера для данного примера:
Расчетные формулы модифицированного метода Эйлера:
Расчетные формулы метода Рунге – Кутта:
| x | y1 | y2 | y3 | точное |
| 0 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 0.1 | 1.2000 | 1.2210 | 1.2221 | 1.2221 |
| 0.2 | 1.4420 | 1.4923 | 1.4977 | 1.4977 |
| 0.3 | 1.7384 | 1.8284 | 1.8432 | 1.8432 |
| 0.4 | 2.1041 | 2.2466 | 2.2783 | 2.2783 |
| 0.5 | 2.5569 | 2.7680 | 2.8274 | 2.8274 |
| 0.6 | 3.1183 | 3.4176 | 3.5201 | 3.5202 |
| 0.7 | 3.8139 | 4.2257 | 4.3927 | 4.3928 |
| 0.8 | 4.6747 | 5.2288 | 5.4894 | 5.4895 |
| 0.9 | 5.7377 | 6.4704 | 6.8643 | 6.8645 |
| 1 | 7.0472 | 8.0032 | 8.5834 | 8.5836 |
y1 – метод Эйлера, y2 – модифицированный метод Эйлера, y3 – метод Рунге Кутта.
Видно, что самым точным является метод Рунге – Кутта.
