Если плоскость фигуры параллельна какой-либо плоскости проекций, т.е. принадлежит плоскости уровня, то на данную плоскость проекций она проецируется без искажения. По-строение ортогональных проекций в этом случае не вызывает затруднений, так как одна проек-ция – сама фигура без искажения, а две других – прямые линии.
В аксонометрии происходит искажение плоских фигур. Например, окружность проециру-ется на аксонометрическую плоскость в эллипс. В изометрии такой эллипс имеет большую ось 1,22, а малую 0,71 диаметра окружности. В диметрии окружность проецируется в эллипсы с осями 1,06 и 0,35, если плоскость ее параллельна горизонтальной и профильной плоскостям проекций.
Если плоскость окружности параллельна фронтальной плоскости проекций, то эллипс имеет большую ось 1,06, а малую 0,95 диаметра окружности. Такой эллипс можно заменить при построении обычной окружностью.
В целях упрощения построений вместо эллипсов строят четырехцентовые овалы. При этом необходимо придерживаться правила, что большая ось эллипса всегда перпендикулярна отсутствующей в данной плоскости аксонометрической оси. Способы построения овалов для изометрии и диметрии приведены на рис. 68 и рис. 69.
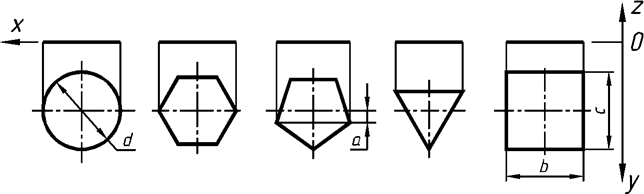
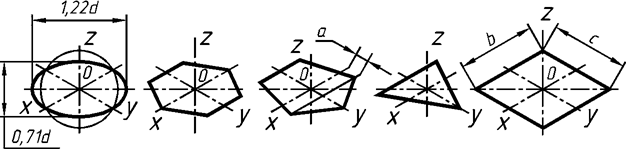
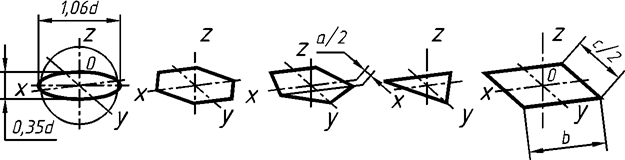
Изображение плоских фигур в ортогональных, изометрических и диметрических прямо-угольных проекциях в плоскости Х0Y показано на рис. 70 а, б, в. Аксонометрия тех же фигур в плоскостях Y0Z и X0Z представлена на рис. 71 а, б. Построение проекций видно из рисунков.
40
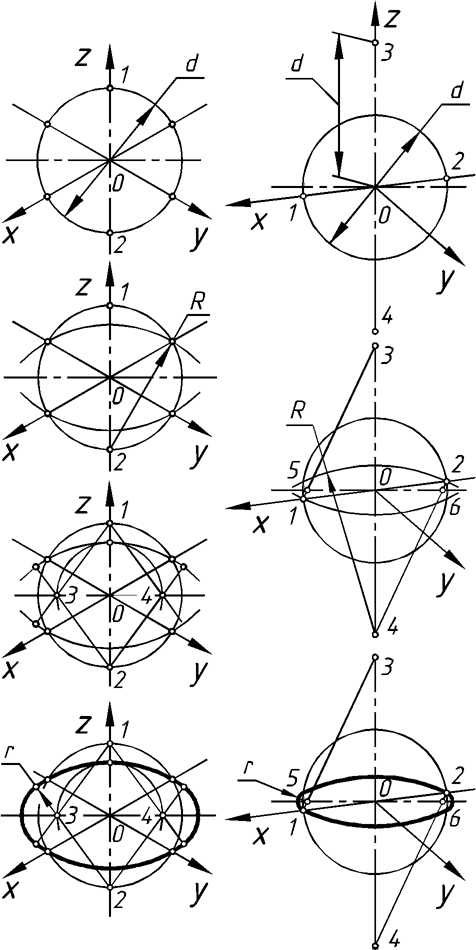
Рис. 68 Рис. 69
41
 |  |  |
а)
 |
б)
 |
в)
Рис. 70
Правило расположения осей овалов
Большая ось овала всегда перпендикулярна той аксонометрической оси, которая не при-надлежит плоскости окружности.
 2020-06-12
2020-06-12 129
129








