Собственные числа и собственные векторы матриц

    Напомним, что собственным числом (собственным значением) и соответствующим ему собственным вектором линейного оператора 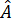 называются такое число 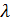и такой ненулевой вектор 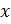, для которых справедливо равенство

.

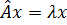    Если переписать это определение в координатной форме через матрицу оператора 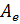 и столбец координат  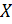в каком-либо базисе, то мы получим аналог определения собственных значений и собственных векторов для матриц:

.

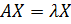Задание 4. Матрица линейного оператора в некотором базисе имеет вид:

.

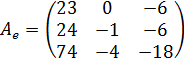Найти собственные значения и собственные векторы данного оператора.

Решение. Учитывая, что матрица оператора 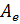 нами уже была введена в примере 3, нам остается только воспользоваться базовыми функциями в R для нахождения собственных значений и собственных векторов для матриц:

d <- eigen(Ae)$values; d         # Собственные значения матрицы Ae

P <- eigen(Ae)$vectors; P        # Собственные векторы Aе, стоящие в столбцах матрицы P

d[1]                                       # Первое собственное значение

P[, 1]                                    # Первый собственный вектор (первый столбец матрицы P)

с результатом:

> d <- eigen(Ae)$values; d # Собственные значения матрицы Ae[1] 3 2 -1> P <- eigen(Ae)$vectors; P # Собственные векторы Aе, стоящие в столбцах матрицы P     [,1] [,2] [,3][1,] 0.2761724 0.2649065 0.2279212[2,] 0.2761724 0.2649065 0.3418817[3,] 0.9205746 0.9271726 0.9116846> d[1]                  # Первое собственное значение[1] 3> P[, 1]               # Первый собственный вектор (первый столбец матрицы P)[1] 0.2761724 0.2761724 0.9205746

Таким образом, мы нашли собственные числа для матрицы 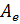, а значит и для оператора 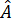. Найденные же собственные векторы матрицы  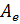являются координатами собственных векторов для оператора  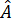в соответствующем базисе.

Важное замечание! Использованная нами функция eigen возвращает в матрице P не просто столбцы собственных векторов, отвечающих собственным значениям. Если количество линейно независимых собственных векторов равно размерности матрицы, то представленные в столбцах линейно независимые собственные векторы образуют нормированный базис (длины векторов равны 1), а в случае симметричной матрицы – образуют ортонормированный базис, т.е. попарно векторы будут еще и ортогональны между собой. При этом сами собственные числа перечисляются по убыванию.

Проверьте, что длины каждого из собственных векторов в нашем случае равны единице, но ортогональности между векторами нет:

sum(P[, 1]^2)          # Например, длина первого собственного вектора

P[, 2] %*% P[, 3]      # Например, скалярное произведение (f2, f3)