Задания для самостоятельной работы

1. Как будет преобразован двумерный вектор  под действием линейного оператора, заданного в каноническом базисе матрицей

.

Сделайте рисунок и попробуйте объяснить словами: что «делает» оператор с векторами.

2. Как изменится график арктангенса на отрезке  под действием линейного оператора с матрицей

,

заданной в каноническом базисе. Ответить на вопрос сравнительным изображением графиков арктангенса и его трансформированного образа.

Указание. Воспользуйтесь аналогией с примером 2, в котором мы поворачивали график функции с помощью матрицы оператора.

3. Найдите собственные значения и собственные векторы для матриц

a)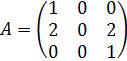

b)

c) . При каких значениях  собственные числа вещественны?

4. Для матрицы получить спектральное и сингулярное разложения и сравнить полученные диагональные виды между собой. Чему равен ранг матрицы?

a)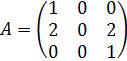

b)  

c)    

5. Привести квадратичную форму

к каноническому виду методом ортогональных преобразований.