Спектральное разложение

    Если матрица линейного оператора вещественная и симметричная, то существует ортонормированный базис построенный из ее собственных векторов, в котором матрица оператора имеет диагональный вид, причем, на главной диагонали стоят соответствующие собственные значения.

    В R получить такое разложение матрицы не представляет никакой проблемы, т.к. возвращаемая матрица из столбцов собственных векторов  eigen(Ae)$vectors сама и является матрицей перехода P к новому ортонормированному базису, который диагонализирует оператор:

Такое разложение матриц часто называют спектральным, а матрицу перехода   P – ортогональным преобразованием, т.к. фактически она определяет собой поворот одного ортонормированного базиса к другому ортонормированному.

Задание 5. Для матрицы линейного оператора в некотором ортонормированном базисе

найти  ортогональное преобразование, приводящее ее к диагональному виду.

Решение. Введем матрицу Ae через excel-формат, найдем ее собственные значения d и собственные векторы P, получим ее диагональный вид D в новом базисе и проверим истинность найденного разложения:

.

Data <- read.table("clipboard",h=FALSE,dec=",",sep = "\t") # Чтение из буфера обмена

Ae <- as.matrix.data.frame(Data); Ae  # Объявляем таблицу чисел Data матрицей Ae в R

d <- eigen(A)$values; d              # Собственные значения матрицы Ae

P <- eigen(A)$vectors; P             # Собственные векторы Aе, стоящие в столбцах матрицы P

P.inv <- solve(P)                      # Обратная матрица к P

D <- P.inv %*% (Ae %*% P); D # Диагонализация квадратной симметричной матрицы Ae

D <- diag(d); D                        # То же самое, но точно. 

Ae                                             # Для сравнения выводим Ae

round(P %*% (D %*% P.inv), 8) # И ее разложение  

Результаты представлены на рисунке 3.

Рис 3.

Интересно, что в этом случае матрица P, состоящая из столбцов ортонормированного базиса, обладает особыми свойствам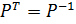и:

и .

 Проверьте это в R для полученной матрицы P. Такие матрицы, кстати, называются ортогональными.

Замечание. Если матрица не симметричная, но линейно независимых собственных векторов хватает для построения базиса, то матрица P также будет приводить к диагональному виду в разложении , но чистым поворотом пространства данное преобразование уже может не быть. Этот случай мы рассмотрели в примере 4 с несимметричной матрицей.