Обратите внимание, что из-за ортогональности матрицы перехода 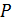 в спектральном разложении, обратная матрица к
в спектральном разложении, обратная матрица к 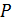 совпадает с транспонированной:
совпадает с транспонированной:
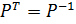 .
.
Таким образом, в этом случае формула преобразования матрицы оператора:
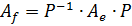
может быть записана в виде:
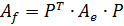 ,
,
что совпадает с преобразованием матрицы квадратичной формы при соответствующей замене базиса. И фактически, таким ортогональным преобразованием 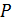 (поворотом пространства) мы приводим квадратичную форму к каноническому виду, причем без растяжений и сжатий. Вот почему ортогональные преобразования и спектральное разложение матриц получили такое широкое применение.
(поворотом пространства) мы приводим квадратичную форму к каноническому виду, причем без растяжений и сжатий. Вот почему ортогональные преобразования и спектральное разложение матриц получили такое широкое применение.
Задание 6. Привести квадратичную форму
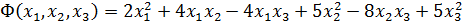
методом ортогональных преобразований к каноническому виду.
Решение. Запишем матрицу квадратичной формы
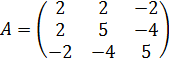 ,
,
после чего нам остается найти ее спектральное разложение. Данную задачу для этой матрицы мы уже решили в предыдущем примере 5 (см. рис.3). Диагональная матрица квадратичной формы при этом получилась
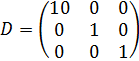 ,
,
что приводит к следующему каноническому виду квадратичной формы в новых переменных:
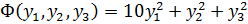 .
.
Сингулярное разложение матриц*
(Singular Values Decomposition, SVD)
Как мы уже отмечали выше, не все вещественные квадратные матрицы допускают спектральное разложение:
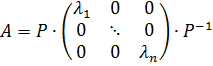 ,
,
где 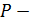 ортогональная матрица, составленная из собственных векторов матрицы
ортогональная матрица, составленная из собственных векторов матрицы 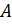 , а
, а 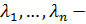 собственные значения матрицы
собственные значения матрицы 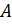 .
.
Одним из частично обобщающих разложений является сингулярное разложение матриц. По теореме Дж. Форсайт для любой квадратной вещественной матрицы 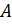 найдутся такие две ортогональные матрицы
найдутся такие две ортогональные матрицы 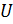 и
и 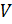 той же размерности, что будет выполняться следующее разложение, называемое сингулярным:
той же размерности, что будет выполняться следующее разложение, называемое сингулярным:
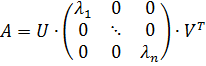 .
.
Причем, всегда можно так выбрать матрицы 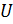 и
и 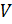 , чтобы числа, стоящие на главной диагонали
, чтобы числа, стоящие на главной диагонали  располагались по убыванию.
располагались по убыванию.
В сингулярном разложении принята следующая терминология: столбцы матрицы 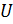 называют левыми сингулярными векторами, а столбцы матрицы
называют левыми сингулярными векторами, а столбцы матрицы 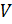 – правыми сингулярными векторами. Значения
– правыми сингулярными векторами. Значения  называют сингулярными значениями матрицы
называют сингулярными значениями матрицы 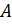 .
.
Для симметричных вещественных неотрицательных квадратных матриц спектральное и сингулярное разложения совпадают.
Замечание. Можно показать, что столбцы матрицы 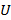 являются собственными векторами матрицы
являются собственными векторами матрицы 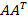 , а квадраты сингулярных чисел
, а квадраты сингулярных чисел  – ее собственными значениями. Аналогично столбцы матрицы
– ее собственными значениями. Аналогично столбцы матрицы 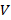 являются собственными векторами матрицы
являются собственными векторами матрицы 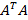 , а квадраты сингулярных чисел так же являются ее собственными значениями.
, а квадраты сингулярных чисел так же являются ее собственными значениями.
Задание 6. Для матрицы
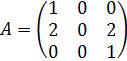
найти ее спектральное разложение.
Решение. Введем матрицу A через excel-формат, найдем ее сингулярные значения d, левую и правую матрицы разложения U и V, получим диагональный вид D в сингулярном разложении и проверим истинность найденного разложения по формуле:
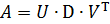 .
.
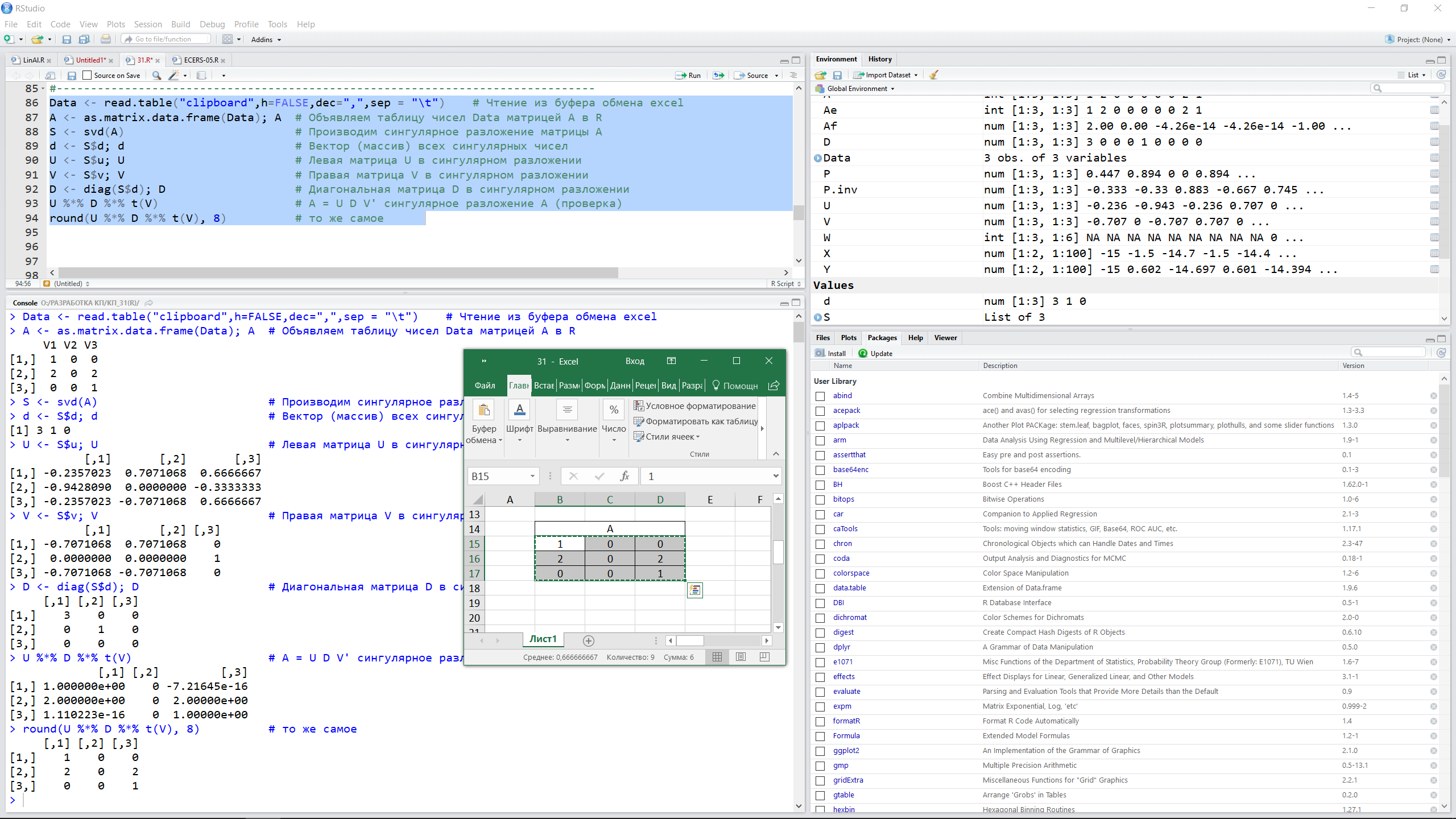
Data <- read.table("clipboard",h=FALSE,dec=",",sep = "\t") # Чтение из буфера обмена excel
A <- as.matrix.data.frame(Data); A # Объявляем таблицу чисел Data матрицей A в R
S <- svd(A) # Производим сингулярное разложение матрицы A
d <- S$d; d # Вектор (массив) всех сингулярных чисел
U <- S$u; U # Левая матрица U в сингулярном разложении
V <- S$v; V # Правая матрица V в сингулярном разложении
D <- diag(S$d); D # Диагональная матрица D в сингулярном разложении
U %*% D %*% t(V) # A = U D V' сингулярное разложение A (проверка)
round(U %*% D %*% t(V), 8) # то же самое, но нагляднее
С результатом, представленном на рисунке 4.
Рис. 4.
Обратите внимание, что полученное сингулярное разложение всегда наглядно отражает ранг матрицы  . Действительно, получающаяся диагональная матрица разложения
. Действительно, получающаяся диагональная матрица разложения
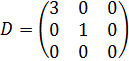
имеет ранг 2, что по свойству сингулярного разложения совпадает с рангом исходной матрицы 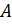 .
.
Замечание. Сингулярное разложение оказывается определено и для неквадратных матриц. Единственное отличие состоит в том, что матрица 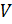 не будет квадратной и уж тем более ортогональной. Попробуйте получить сингулярное разложение для матрицы:
не будет квадратной и уж тем более ортогональной. Попробуйте получить сингулярное разложение для матрицы:
A <- matrix(1:12, 3, 4, byrow = TRUE); A
т.е. найти соответствующие матрицы 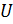 ,
, 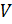 и
и 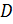 . Обязательно проверьте результат – сингулярное разложение матрицы должно совпадать с самой матрицей:
. Обязательно проверьте результат – сингулярное разложение матрицы должно совпадать с самой матрицей:
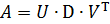 .
.
 2020-06-12
2020-06-12 147
147








