Выражение для скорости гомогенной химической реакции имеет вид
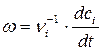 , (1.1)
, (1.1)
где сi – молярная концентрация реагента,
νi – стехиометрические коэффициенты в уравнении реакции
с учетом правила знаков,
t – время.
Для односторонних реакций вида ν1А + ν2В → продукты справедливо равенство
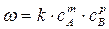 , (1.2)
, (1.2)
характеризующее зависимость скорости реакции от концентрации реагирующих веществ. В этом уравнении k – константа скорости реакции; m и р – коэффициенты, называемые порядками реакции по веществам А и В соответственно. Суммарный показатель степени n = m + р называется общим порядком реакции. При n =1 имеем дело с реакцией первого порядка, при n =2 – второго и так далее.
Для реакции i – го порядка с учетом (1.1) и (1.2) можно записать
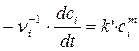 или
или 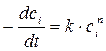 , (1.3)
, (1.3)
где 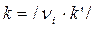 .
.
Интегрирование в переделах 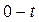 и
и 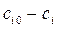 , дает (кроме n =1)
, дает (кроме n =1)
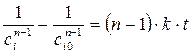 . (1.4)
. (1.4)
Откуда
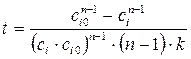 . (1.5)
. (1.5)
Для случая, когда n =1
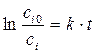 , (1.6)
, (1.6)
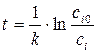 . (1.7)
. (1.7)
Обозначим через 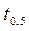 время половинного превращения, т.е. тот интервал времени, за который текущая концентрация
время половинного превращения, т.е. тот интервал времени, за который текущая концентрация 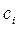 становится равной половине начальной
становится равной половине начальной 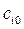 (кроме n =1):
(кроме n =1): 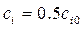 . Тогда
. Тогда
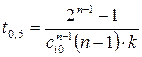 . (1.8)
. (1.8)
Для случая, когда n =1
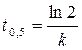 . (1.9)
. (1.9)
Проведя определение половинного времени реакции 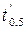 и
и 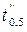 в двух опытах при T = const, но различных начальных концентрациях
в двух опытах при T = const, но различных начальных концентрациях 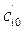 и
и 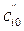 , можно рассчитать порядок реакции:
, можно рассчитать порядок реакции:
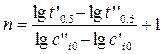 . (1.10)
. (1.10)
Зависимость константы скорости реакции от температуры выражается уравнением Аррениуса
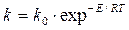 , (1.11)
, (1.11)
где Е – энергия активации,
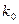 – постоянный коэффициент, или предэкспоненциальный множитель.
– постоянный коэффициент, или предэкспоненциальный множитель.
Указанная зависимость объясняется тем, что для осуществления элементарного акта взаимодействия при соударении молекул последние должны обладать некоторой избыточной энергией по сравнению со средней энергией реагирующих молекул. Эта энергия расходуется на частичный или полный разрыв "старых" связей, так как любая химическая реакция сводится к разрушению одних и возникновению других связей. Поскольку число частиц с избытком энергии увеличивается с ростом температуры по закону Больцмана, то и скорость реакции возрастает при увеличении температуры по экспоненциальному закону.
После логарифмирования отношения двух форм уравнения (1.11) при 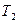 и
и 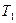 получим
получим
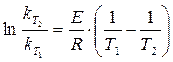 . (1.12)
. (1.12)
Зная константы скорости 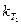 и
и 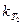 при
при 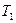 и
и 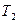 , можно рассчитать энергию активации
, можно рассчитать энергию активации
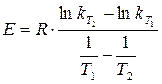 . (1.13)
. (1.13)
 2020-06-12
2020-06-12 114
114








