Смысловое содержание используемых величин

1. Математическое ожидание или среднее значение:

где:

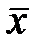-  – математическое ожидание или среднее значение признака;

- х_i= х₁, х₂, х₃, … х_n – реализации (даты, количественные значения) получаемые в результате проведения опытов

- n – численность совокупности – количество учтенных наблюдений, замеров;

- i – порядковый номер единицы учета в совокупности.

 

Величина 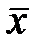 определяет место расположения «центра тяжести» статистической совокупности на числовой оси. Название «математическое ожидание» связано с тем, что  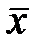служит центром ожидаемой концентрации возможных значений случайной величины.

2. Дисперсия S² или средний квадрат отклонений характеризует рассеивание случайной величины около её среднего значения.

где:

- S² – дисперсия (в некоторых публикациях обозначается символом σ²);

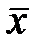-  - математическое ожидание или среднее значение признака;

- х_i= х₁, х₂, х₃, … х_n – реализации (даты, количественные значения) получаемые в результате проведения опытов;

- n – численность совокупности – количество учтенных наблюдений, замеров;

- i – порядковый номер единицы учета в совокупности.

 

3. Ввиду того, что размерность дисперсии не совпадает с размерностью изучаемой случайной величины – равна её квадрату, более удобной и приемлемой характеристикой величины рассеяния является среднеквадратическое отклонение, определяемое формулой (соотношением):

 

Сравнение двух случайных величин или двух статистических совокупностей по величине среднеквадратического отклонения правомерно лишь при условии, что их математические ожидания – средние значения – равны.

 

4. В общем случае (когда математические ожидания могут быть и не равны между собой) для сравнения необходимо использовать коэффициент вариации (Cv):

Величина Cv показывает, какую долю от среднего арифметического составляет среднеквадратическое отклонение. Эта величина может быть выражена в долях от среднего – безразмерной статистики, так и в процентах, тогда в формулу вводится коэффициент «100».

 

5. Для характеристики асимметрии распределения – распределения значений случайной величины относительно 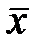 – можно использовать коэффициент асимметрии (A):

где:

- .

 

При А >0 асимметрия положительная (левая), при А<0 – отрицательная – правая. По величине коэффициента асимметрии можно судить о преобладании в выборке относительно малых значений случайной величины (А >0) или – больших (А<0).

 

6. Степень заостренности распределения случайной величины можно характеризовать при помощи показателя эксцесса (Е):

 

7. Для среднего значения, коэффициента асимметрии и показателя эксцесса рассчитывают и их среднеквадратические ошибки:

 

Ошибка коэффициента асимметрии:

 

Ошибка показателя эксцесса:

 

Среднеквадратические ошибки указывают на возможную амплитуду изменений соответствующих показателей (статистик), вычисленных по n опытным значениям.

8. Для характеристики точности опыта (выполненного эксперимента или наблюдения) рассчитывают так называемый показатель точности опыта:

 

Показатель иногда называют относительной ошибкой. Вместе с тем некоторые специалисты (Лейтас, 1983, стр. 23) сомневаются в «полезности» использования данного показателя с целью оценок точности опыта на том основании, что значение оценки Р непосредственно зависит от величины математического ожидания (среднего значения) самой статистической совокупности, подвергаемой статистическому анализу. Однако несостоятельность таких «опасений» авторов очевидна: на стр. 22 ими приведены формулы, в расчетах которых предусмотрены аналогичные схемы отношений некоторого параметра к среднему значению признака в статистической совокупности (коэффициент вариации).