Смысловое содержание используемых величин

1. Лимит или предел – это одно из ключевых понятий вариационной статистики и математики в целом. Лимитом (lim.) является некоторая постоянная величина (константа), к которой неограниченно приближается некоторая переменная величина (переменная). При этом изменения переменной могут происходить как в сторону её увеличения, так и в сторону уменьшения, в соответствии с чем она будет стремиться к абсолютному максимуму или абсолютному минимуму.

- lim. – лимит или предел значений вообще.

- Amax – абсолютный максимум значений признака;

- Amin – абсолютный минимум значений признака.

 

2. Диапазон значений – это ограниченная лимитами совокупность потенциальных значений признака, которые тестируемый признак может принимать в процессе изменения его величины. Количественное выражение интервала лимитов или диапазона (Δ lim.) значений признака представляет собой разность между величинами его абсолютного максимума (Maximum – Amax.) и абсолютного минимума (Minimum – Amin.):

Δ lim = Amax – Amin,

где:

- Δ lim – абсолютный диапазон или интервал значений признака;

- Amax – абсолютный максимум значений признака;

- Amin – абсолютный минимум значений признака.

 

3. Среднее линейное отклонение характеризует абсолютную меру разброса значений признака в статистической совокупности и вычисляется по нижеследующему алгоритму:

 

,

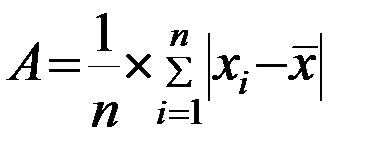где:

- А – среднее линейное отклонение;

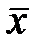-  – математическое ожидание или среднее значение признака;

- х_i= х₁, х₂, х₃, … х_n – реализации (даты, количественные значения) получаемые в результате проведения опытов;

- n – численность совокупности – количество учтенных наблюдений, замеров;

- i – порядковый номер единицы учета в совокупности.

 

4. Дисперсия – это рассеяние значений признака, разброс значений того или иного признака объектов некоторой статистической совокупности.

5. Варианса – это мера дисперсии (изменчивости) признака у изучаемых объектов в их совокупности. Дисперсия (S²) или средний квадрат отклонений характеризует рассеивание случайной величины около её среднего значения.

где:

- S² – дисперсия (в некоторых публикациях обозначается символом σ²);

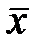-  - математическое ожидание или среднее значение признака;

- х_i= х₁, х₂, х₃, … х_n – реализации (даты, количественные значения) получаемые в результате проведения опытов;

- n – численность совокупности – количество учтенных наблюдений, замеров;

- i – порядковый номер единицы учета в совокупности.

 

6. Ввиду того, что размерность дисперсии не совпадает с размерностью изучаемой случайной величины – равна её квадрату, более удобной и приемлемой характеристикой величины рассеяния является среднеквадратическое отклонение, определяемое формулой (соотношением):

,

где:

- S – среднеквадратическое или стандартное отклонение (в некоторых публикациях обозначается символом σ);

- S² – дисперсия (в некоторых публикациях обозначается символом σ²).

 

7. Следует помнить, что сравнение двух случайных величин или двух статистических совокупностей по величине среднеквадратического отклонения правомерно лишь при условии, что их математические ожидания – средние значения – равны. В общем случае, когда математические ожидания могут быть и не равны между собой (что нередко наблюдается в совокупностях лесоводственных объектов) для сравнительных оценок характера изменчивости необходимо использовать парный коэффициент вариации Пирсона (Cv):

 

Величина Cv показывает, какую долю от среднего арифметического составляет среднеквадратическое отклонение. Эта величина может быть выражена в долях от среднего – безразмерной статистики, так и в процентах, тогда в формулу вводится коэффициент «100». Вычисляется только для количественных данных. В отличие от среднеквадратического или стандартного отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. При этом, как считал К. Пирсон (Pirson, 1896), предложивший указанный коэффициент, он более эффективно описывает изменчивость как таковую по сравнению с вышеозначенными абсолютными показателями варьирования, такими как дисперсия или среднеквадратическое отклонение.

 

8. Линейный коэффициент вариации (С _А) в смысловом и алгоритмическом плане близок к парному коэффициенту вариации Пирсона (Cv) и также вычисляется только для количественных величин по следующей формуле:

 

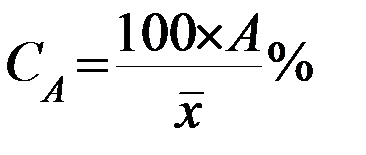
где:

- С_А – линейный коэффициент вариации;

- А – среднее линейное отклонение (алгоритм вычисления приведен выше);

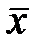-  - математическое ожидание или среднее значение признака;

- х_i= х₁, х₂, х₃, … х_n – реализации (даты, количественные значения) получаемые в результате проведения опытов;

- n – численность совокупности – количество учтенных наблюдений, замеров;

- i – порядковый номер единицы учета в совокупности.

 

Линейный коэффициент корреляции иногда называю относительным отклонением по модулю, имея в виду, что в основе его вычисления лежит среднее линейное отклонение, устанавливаемое как средняя сумма модулей отклонения вариант от среднего значения признака. Выражают линейный коэффициент вариации также, как и обычный коэффициент вариации: либо в долях от среднего – безразмерной статистикой, либо в процентах, тогда в формулу также вводится коэффициент «100».  

 

9. Относительный размах вариации (коэффициент осцилляции) – это одна из описательных статистик, характеризующая изменчивость признака. Коэффициент осцилляции показывает, какую долю от среднего значения признака составляет абсолютный диапазон. Поскольку и абсолютный диапазон и среднее значение признака выражены в одних единицах измерения, результирующее значение относительного размаха вариации безразмерно. Как правило, его выражают либо в долях от единицы, либо в процентах, тогда в алгоритм записи вводят коэффициент 100, что и представлено на нижеследующем алгоритме:

Р = 100 × (Amax – Amin) / М %,

где:

- Р – относительный размах вариации;

- Amax – абсолютный максимум значений признака;

- Amin – абсолютный минимум значений признака.

- M – среднее арифметическое значение признака или математическое ожидание, его также обозначают символом ;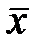

- 100 – поправочный коэффициент перевода значений доли в проценты.