Парная корреляция. Как было установлено выше, корреляция – это статистическая нефункциональная взаимозависимость двух или более линейных случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). Для раскрытия смыслового содержания этого выражения рассмотрим пример.
ПРИМЕР 1. Общеизвестно (учебники лесоведения, лесоводства лесной таксации и др.), что в насаждении большей высоте ствола дерева соответствует его больший диаметр и наоборот. Как правило, с увеличением высоты ствола (как таксационного показателя) увеличивается и его диаметр (как таксационный показатель) и наоборот. Вместе с тем, также общеизвестны случаи, когда у деревьев с одинаковой высотой фиксируются различные диаметры или, когда у деревьев с одинаковым диаметром наблюдается разная высота (высота ствола в пределах одной ступени толщины). Более того, нередко в насаждении можно (обнаружить) наблюдать ситуацию, когда большей высоте таксируемого дерева соответствует меньший по сравнению с другими диаметр. Все эти случает можно зафиксировать в одном насаждении. В такой ситуации говорить о функциональной или пропорциональной зависимости не приходится. Можно лишь обозначить тенденцию во взаимозависимости одного показателя от другого, которая может в большей или меньшей мере приближаться к пропорциональной. Такая связь между переменными или, как их еще называют, случайными величинами является корреляционной.
Термин «корреляция» происходит от латинского слова correlatio, которое означает «соотношение, взаимосвязь». В лесоводственных исследованиях наиболее часто используют парный коэффициент корреляции Пирсона, алгоритм вычисления которого представлен ниже:
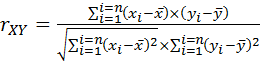 ,
,
где:
- rXY – парный коэффициент корреляции признака X и признака Y;
- 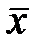 – математическое ожидание или среднее значение первого из двух признаков;
– математическое ожидание или среднее значение первого из двух признаков;
- хi= х1, х2, х3, … хn – реализации (даты или количественные значения) первого из двух признаков, получаемые в результате проведения опытов;
-  – математическое ожидание или среднее значение второго из двух признаков;
– математическое ожидание или среднее значение второго из двух признаков;
- уi= у1, у2, у3, … уn – реализации (даты или количественные значения) второго из двух признаков, получаемые в результате проведения опытов;
- n – численность каждой из совокупностей – количество учтенных в ней наблюдений, замеров;
- i – порядковый номер единицы учета в совокупности: i = 1… n.
При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция – это корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях – это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи, например, для независимых случайных величин.
Парный коэффициент корреляции Пирсона выражается в долях от единицы и всегда находится в интервале значений от −1 до 1. Оценки коэффициента корреляции можно выражать в процентах, тогда интервалом его значений будет +100 % … –100 %. Понятно, что при этом общий смысл оценок не изменится. Также следует учитывать то, что отсутствие корреляции между двумя случайными величинами (коэффициент корреляции минимален, недостоверен или равен нулю) ещё не значит, что между ними нет никакой связи. Например, зависимость может иметь сложный нелинейный характер, который корреляция не выявляет. Корреляция Пирсона есть мера линейной связи между двумя переменными. Она позволяет определить, насколько пропорциональна изменчивость этих двух переменных. Если переменные пропорциональны друг другу, то графически связь между ними можно представить в виде прямой линии с положительным (прямая пропорция) или отрицательным (обратная пропорция) наклоном. Кроме того, если известна пропорция между переменными, заданная уравнением графика прямой линии:
Статистическая значимость коэффициента корреляции определяется, исходя из результатов сопоставления величины его стандартной статистической ошибки с величиной самого коэффициента. Величину этой ошибки вычисляют по следующей общепринятой формуле:
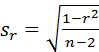 ,
,
где:
- sr – стандартная ошибка коэффициента корреляции;
- r – коэффициент корреляции;
- n – численность выборки или число парных учетов, по которым вычислен выборочный коэффициент корреляции.
Критерий существенности коэффициента корреляции рассчитывают, используя полученную величину стандартной ошибки, по следующей формуле:
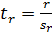 ,
,
где:
- t r – критерий существенности коэффициента корреляции;
- sr – стандартная ошибка коэффициента корреляции;
- r – коэффициент корреляции.
Поскольку расчетное значение коэффициента корреляции есть случайное значение его сопоставляю с табличным значение на 5-процентном уровне значимости. Если расчетное значение t-критерия меньше табличного при заданном числе степеней свободы и на установленном уровне значимости, статистическая значимость наблюдаемой взаимосвязи - отсутствует. Если больше или равно, то корреляционная связь считается статистически значимой.
Частная корреляция. Очень часто две переменные (признак X и признак Y) коррелируют друг с другом только за счет того, что обе они согласованно меняются под влиянием некоторой третьей переменной (Z). Иными словами, на самом деле связь между соответствующими свойствами отсутствует, но проявляется в статистической взаимосвязи (корреляции) под влиянием общей причины. Для того, чтобы вскрыть истинный характер взаимозависимости между признаками такого комплекса и для оценки реальной степени взаимозависимости между такими переменными применяют коэффициент частной корреляции (Partial Correlation). Для вычисления оценок частной корреляции достаточно знать три коэффициента корреляции Пирсона между переменными X, Y и Z: rXY, rXZ и rYZ. Имея указанные значения трех парных коэффициентов корреляции, частные коэффициенты корреляции рассчитывают по нижеприведенным формулам:
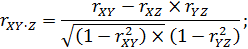

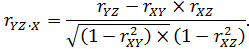
В алгоритмической записи для первого уравнения имеем:
- rXY ‧ Z – частный коэффициент корреляции между переменными X и Y, корреляционная зависимость между которыми изучается, и переменной Z, влияние которой элиминировано (исключено);
- X – переменная, коррелирующая с признаком Y и не коррелирующая с признаком Z;
- Y – переменная, коррелирующая с признаком X и не коррелирующая с признаком Z;
- Z – переменная, влияние которой на признак X и на признак Y исключено.
В алгоритмической записи для второго и третьего уравнения логика сохраняется.
Статистическая значимость частных коэффициентов корреляции также определяется, исходя из результатов сопоставления величины его стандартной статистической ошибки с величиной самого коэффициента. Величину этой ошибки вычисляют по той же формуле:
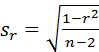 ,
,
где:
- sr – стандартная ошибка коэффициента корреляции;
- r – коэффициент корреляции;
- n – численность выборки или число парных учетов, по которым вычислен выборочный коэффициент корреляции.
Критерий существенности коэффициента корреляции рассчитывают, используя полученную величину стандартной ошибки, по следующей формуле:
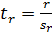 ,
,
где:
- t r – критерий существенности коэффициента корреляции;
- sr – стандартная ошибка коэффициента корреляции;
- r – коэффициент корреляции.
Поскольку расчетное значение коэффициента корреляции есть случайное значение его сопоставляю с табличным значение на 5-процентном или 1-процентном уровне значимости. Если расчетное значение t-критерия меньше табличного при заданном числе степеней свободы и на установленном уровне значимости, статистическая значимость наблюдаемой взаимосвязи - отсутствует. Если больше или равно, то корреляционная связь считается статистически значимой.
Множественная корреляция. Если на величину какого-либо исследуемого признака (например, масса шишек), представляющего собой переменную или случайную величину, одновременно влияют другие признаки (например, дина и диаметр шишек), между которыми также могут существовать корреляционные связи, то имеет место множественная корреляция. Иными словами, при наличии линейной связи между результативным и несколькими факторными признаками лесоводственных объектов, а также между каждой парой факторных признаков вычисляется множественный коэффициент корреляции. При этом коэффициент множественной корреляции рассматривается как мера для численного определения тесноты линейной корреляционной связи между одной случайной величиной и некоторым множеством других случайных величин. Можно сказать, что он используется для измерения тесноты связи при множественной корреляционной зависимости между случайными величинами в их некотором множестве (их число больше 2).
Наиболее просто анализируется множественная корреляция, представляющая собой линейную зависимость между тремя признаками, когда один из них (Y) рассматривается как результативный или как функция, а два других (X и Z) играют роль аргументов. Числовые значения множественного коэффициента корреляции легко вычисляются при наличии значений парных коэффициентов корреляции (rXY, rXZ и rYZ.) по приведенным ниже формулам:
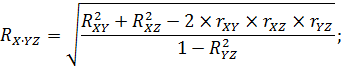
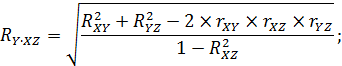

В алгоритмической записи для первого уравнения имеем:
- rX‧YZ – множественный коэффициент корреляции между результативной переменной X (выступающей в роли функции) и влияющими переменными Y и Z (выступающими в роли активных факторов влияния – аргументов);
- X – результативная переменная, значения которой формируются под совместным влиянием и признака Y, и признака Z (одновременно коррелирующая и с признаком Y и с признаком Z);
- Y – одна из двух переменных, коррелирующих с признаком X;
- Z – другая из двух переменных, коррелирующих с признаком X; переменная, влияние которой на признак X и на признак Y исключено.
В алгоритмической записи для второго и третьего уравнения логика сохраняется.
Множественный коэффициент корреляции (RX ‧ YZ) выражается в долях от единицы, изменяется в пределах от 0 до 1 и по определению всегда положителен. Когда величина множественного коэффициента корреляции (RX ‧ YZ) приближается к единице (к 1), степень линейной связи всех трех признаков возрастает. Следует учитывать, что между коэффициентом множественной корреляции (RX ‧ YZ) и двумя коэффициентами парной корреляции тех же признаков, такими как rXY, rXZ, существует непременное соотношение, согласно которому ни один из указанных парных коэффициентов корреляции (ни rXY, ни rXZ) не может превышать по абсолютной величине множественный коэффициент корреляции – RX ‧ YZ.
И в случае множественной корреляции статистическая значимость коэффициентов корреляции определяется, исходя из результатов сопоставления величины их стандартной статистической ошибки с величиной самих коэффициентов. Величину этой ошибки вычисляют по следующей общепринятой формуле:
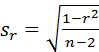 ,
,
где:
- sr – стандартная ошибка коэффициента корреляции;
- r – коэффициент корреляции$
- n – численность выборки или число парных учетов, по которым вычислен выборочный коэффициент корреляции,
Критерий существенности коэффициента корреляции рассчитывают, используя полученную величину стандартной ошибки, по следующей формуле:
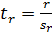 ,
,
где:
- t r – критерий существенности коэффициента корреляции;
- sr – стандартная ошибка коэффициента корреляции;
- r – коэффициент корреляции.
Поскольку расчетное значение коэффициента корреляции есть случайное значение его сопоставляю с табличным значение на 5-процентном или 1-процентном уровне значимости. Если расчетное значение t-критерия меньше табличного при заданном числе степеней свободы и на установленном уровне значимости, статистическая значимость наблюдаемой взаимосвязи - отсутствует. Если больше или равно, то корреляционная связь считается статистически значимой.
Ранговая корреляция. Если обе переменные (X и Y), между которыми изучается связь, представлены в порядковой шкале, или одна из них – в порядковой, а другая – в метрической, то применяются коэффициенты ранговой корреляции: r-Спирмена (rS) или τ-Кенделла (τK). И тот, и другой коэффициент требует для своего применения предварительного ранжирования обеих переменных. Ранговая корреляция представляет собой метод корреляционного анализа, отражающий соотношение между переменными, упорядоченными по возрастанию их значений (ранжированными в порядке возрастания или убывания). Вообще-то ранжирование может быть и прямым, и обратным, но в обязательном порядке одинаковым для обеих переменных: либо от меньших значений признака к большим, либо наоборот. В связи с тем, что ранговый коэффициент корреляции является инструментом непараметрического анализа, при вычислении его величины проверка на нормальность распределения значений признака в совокупности не требуется. Ранги – это порядковые номера единиц совокупности в ранжированном ряду. Если одновременно ранжировать совокупность по двум признакам, связь между которыми изучается, то полное совпадение рангов означает максимально тесную прямую связь, а полная противоположность рангов – максимально тесную обратную связь. Для практических целей использование ранговой корреляции весьма полезно. Например, если установлена высокая ранговая корреляция между двумя качественными признаками (характеристиками типов лесорастительных условий или, формой плодов и формой листовых пластинок), то анализировать лесные участки, представляющие их, достаточно только по одному из признаков, что удешевляет и ускоряет выполняемую в таком порядке работу. Однако здесь важно иметь в виду, что осуществление ранговой корреляции возможно только для признаков измеряемых единицами порядковой шкалы или шкал более высокого уровня (интервальной шкалой или шкалой отношений). Для признаков, единицы категорий которых измеряются номинальной шкалой (типы леса, характеристики грубой коры деревьев и т.п.), ранговая корреляция неприменима.
Коэффициент ранговой корреляции Спирмена – это математическая мера для определения фактической степени параллелизма между двумя количественными рядами изучаемых признаков и получения оценки тесноты установленной связи с помощью количественно выраженного коэффициента. Данный критерий был разработан и предложен для проведения одной из форм корреляционного анализа в 1904 году Чарльзом Эдвардом Спирменом, английским психологом, профессором Лондонского и Честерфилдского университетов. Коэффициент корреляции r-Спирмена (Spearman's rho) равен коэффициенту парной корреляции r-Пирсона, вычисленному для двух рядов ранговых оценок (порядковых номеров в ранжированном ряду), присваиваемых соответствующему текущему значению каждой из двух переменных. При вычислении коэффициента ранговой корреляции Спирмена оперируют показателями рангов (порядковыми номерами в ранжированном ряду), которые получают текущие значения в зависимости от их порядкового номера в ранжированном ряду каждой их из двух коррелирующих переменных Х и Y.
Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале (изначально представленными в единицах любой шкалы, измерение с помощью которой, обеспечивает в последующем выполнение процедуры ранжирования). При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности (распределение является нормальным или не относится к таковому). В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и с помощью количественно выраженного коэффициента дается оценка тесноты установленной связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых значений изучаемых переменных.
Если члены некоторой совокупности (выборки) численностью n были ранжированы сначала по признаку (переменной) X, затем – по признаку (переменной) Y, то оценку формы и степени корреляции между переменными Х и Y можно получить, используя алгоритм вычисления парного коэффициента корреляции Пирсона для двух рядов рангов. При условии отсутствия связей в рангах (т. е. отсутствия повторяющихся рангов) по той и другой переменной, формула для r-Пирсона может быть существенно упрощена в вычислительном отношении и преобразована в формулу, известную как алгоритм вычисления r-Спирмена:
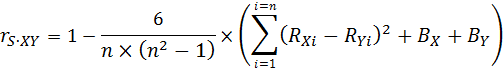
где:
- rS‧XY – коэффициент ранговой корреляции между ранжированными рядами значений переменной (признаком) X и переменной (признаком) Y;
- X – одна из двух переменных, коррелирующая с признаком Y;
- Y – одна из двух переменных, коррелирующая с признаком X;
- RXi – ранг (порядковый номер в ранжированном ряду), присвоенный текущему значению (xi) переменной X в не ранжированном ряду её значений;
- RYi – ранг (порядковый номер в ранжированном ряду), присвоенный текущему значению (yi) переменной Y в не ранжированном ряду её значений;
- n – число пар значений двух сравниваемых признаков, адекватное численности каждой из совокупностей – количеству учтенных в каждой их них наблюдений или замеров;
- i – порядковый номер единицы учета рангов в их совокупности – порядковый номер пары рангов: i = 1… n.
В ситуации, когда в ранжированном ряду присутствуют одинаковые значения переменной, ранг каждого из этих значений не может быть определен однозначно, поскольку ранг – это порядковый номер – целое число. В таких случаях каждому из одинаковых значений ранжированного ряда присваивается одинаковая оценка ранга. Она вычисляется как среднее арифметическое того или иного количества последовательных ранговых оценок, которые могли бы быть присвоены элементам ранжированного ряда с одинаковыми значениями. Это можно рассмотреть на примере, в котором некоторой части последовательных ранговых оценок (например: «3», «4» и «5») соответствуют одинаковые значения переменной. Среднее арифметическое ранговых оценок равно «4», поскольку (3+4+5)/3=4. Все три одинаковых значения переменной в данной ситуации получат условную ранговую оценку «4». При этом легко заметить, что общая сумма ранговых оценок ранжированного ряда не изменится. Такая усредненная ранговая оценка не всегда оказывается целым числом. В частности, когда одинаковое значение имеют только две последовательные позиции в ранжированном ряду (например: «3» и «4»), их средняя оценка составит «3,5» или (3+4)/2=3,5. Этот условный ранг будет присвоен каждому из двух одинаковых значений. И в этом случая общая сумма ранговых оценок ранжированного ряда не изменится. В больших выборках, формирование которых характерно для лесоводственных исследований, таких групп объектов с одинаковыми значениями признака в составе ранжированного ряда может быть несколько. Причем для каждого признака количество таких групп индивидуально и может не совпадать. Их наличие предполагает необходимость вычисления поправок на объединение рангов и усреднение их порядковых оценок. Действие направлено на повышение точности результатов. В этом случае расчетная формула приобретает вид:
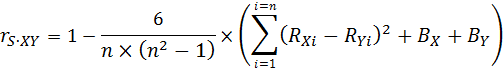
где:
- BX – поправка на объединение рангов в ряду переменной X;
- BY – поправка на объединение рангов в ряду переменной Y;
Величина поправок для каждого признак (каждой из переменных) устанавливается по унифицированной формуле (например, для переменной X):
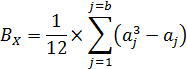
где:
- X – одна из двух переменных, коррелирующая с неким признаком Y;
- аj – число позиций (рангов) в каждой группе объединенных рангов – численность каждой j -той группы объединенных рангов для признака X;
- b – число групп объединенных рангов в ранжированном ряду для признака X;
- j – порядковый номер группы объединенных рангов в ранжированном ряду для признака X: j = 1… b.
Для переменной Y смысловое содержание формулы не меняется.
Вместе с тем, как показывает опыт, результаты, полученные по скорректированной формуле для рядов с наличием связанных рангов, мало отличаются от результатов, полученных по формуле для рядов, состоящих из неповторяющихся рангов. Поэтому на практике, в расчетах, как для неповторяющихся, так и для повторяющихся рангов, нередко применяют нескорректированную формулу, признавая достаточной точность вычислений, которую она обеспечивает.
Статистическая значимость коэффициента ранговой корреляции, как и в рассмотренных ранее случаях, определяется, исходя из результатов сопоставления величины его стандартной статистической ошибки с величиной самого коэффициента. Величину этой ошибки также вычисляют по следующей общепринятой формуле:
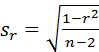 ,
,
где:
- sr – стандартная ошибка коэффициента корреляции;
- r – коэффициент корреляции;
- n – численность выборки или число парных учетов, по которым вычислен выборочный коэффициент корреляции.
Критерий существенности коэффициента корреляции рассчитывают, используя полученную величину стандартной ошибки, по следующей формуле:
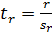 ,
,
где:
- t r – критерий существенности коэффициента корреляции;
- sr – стандартная ошибка коэффициента корреляции;
- r – коэффициент корреляции.
Поскольку расчетное значение коэффициента корреляции есть случайное значение его сопоставляю с табличным значение на 5-процентном уровне значимости. Если расчетное значение t-критерия меньше табличного при заданном числе степеней свободы и на установленном уровне значимости, статистическая значимость наблюдаемой взаимосвязи - отсутствует. Если больше или равно, то корреляционная связь считается статистически значимой.
В настоящее время сферы применения коэффициента ранговой корреляции Спирмена достаточно широки и распространяются, в том числе, на лесное и лесопарковое хозяйство. Прежде всего он используется для выявления факта наличия, и оценки тесноты и направленности связи между двумя рядами сопоставляемых количественных показателей лесоводственных объектов. Величина коэффициента ранговой корреляции Спирмена (rS), выражается в долях от единицы и лежит в интервале от +1 до -1. Он может быть положительным и отрицательным, характеризуя направленность связи между двумя признаками, измеренными в ранговой шкале. При этом, чем ближе модуль коэффициента корреляции к единице, тем более сильной является связь между измеряемыми величинами. Если rS=1, имеет место строго прямая связь; при rS = -1 – строго обратная связь. Если же коэффициент корреляции равен нулю (rS=0), то связь между величинами признается отсутствующей. Иными словами, если ранги показателей, упорядоченных по степени возрастания или убывания, в большинстве случаев совпадают или, когда большему значению одного показателя соответствует большее значение другого, например, при сопоставлении ранговых оценок высоты дерева с соответствующими ранговыми значениями объема, диаметра или массы его ствола), делается вывод о наличии прямой корреляционной связи. Если ранги показателей имеют противоположную направленность, когда большему значению одного рангового показателя соответствует меньшее значение другого, например, при сопоставлении возраста и темпов прироста стволовой древесины в спелых и перестойных насаждениях), то говорят об обратной связи между показателями.
Важным и, конечно же, положительным свойством коэффициента ранговой корреляции Спирмена выступает то, что при его вычислении сопоставляемые показатели могут быть измерены как единицами интервальной шкалы (например, оценки общей комбинационной способности) или шкалы отношений (например, число единиц благонадежного подроста на 1 га), так и в единицах порядковой шкалы (например, баллы ранговой экспертной оценки морозостойкости деревьев и кустарников по Э.Л. Вольфу, (Вольф, 1915): от 1 до 5 или баллы ранговой экспертной оценки урожайности насаждений по В.Г. Капперу, 1936 (Каппер, 1936): от 0 до 5). Однако следует учитывать, что эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины.
 2020-06-12
2020-06-12 130
130








