Тема: «Исследование ковариации между признаками лесоводственных объектов»
Ключевые слова: ковариация, коэффициент ковариации, взаимозависимость, переменные величины, дисперсия.
Форма проведения занятия – аудиторные занятия, лабораторная работа.
Бюджет времени – 4 часа.
Количество двухчасовых занятий – 4.
Распределение бюджета времени:
- 1 час на освоение смыслового содержания понятий и теоретических основ вычисления статистических величин ковариационного анализа;
- 3 час на самостоятельное практическое освоение алгоритмов вычисления значений парных коэффициентов ковариации.
Дидактический материал, необходимый для проведения данной лабораторной работы, приведен в файле электронных таблиц Microsoft Excel – «Ковариация» (Приложение 8.1).
Вводная часть
Исследование ковариационных связей состоит в одновременном анализе сумм квадратов и сумм произведений отклонений двух и более переменных от их средних. В лесном и лесопарковом хозяйстве ковариационный анализ используют при планировании опыта и статистической обработке его результатов. Он позволяет установить и количественно оценить соотношение между вариацией некоторой зависимой переменной, например, объем ствола отдельного дерева и варьированием сопутствующей опыту. Иногда ковариационный анализ рассматривают как распространение методов дисперсионного анализа на случаи с несколькими переменными
Ковариация – это мера линейной зависимости двух случайных величин.
В статистике под ковариацией понимают среднее произведение отклонений вариант двух переменных от их средних. Расчетная формула этого показателя имеет вид:

или:
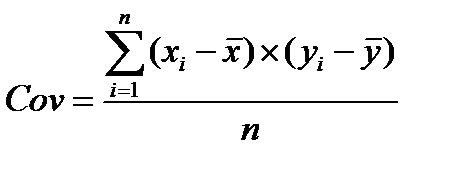 ,
,
где:
- X – одна из двух переменных, взаимосвязанная с неким признаком Y;
- Y – одна из двух переменных, взаимосвязанная с неким признаком X;
- Cov(X;Y) – оценка ковариации двух признаков (переменных величин X и Y) – коэффициент их ковариации;
- 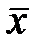 – математическое ожидание или среднее значение первого из двух признаков (X);
– математическое ожидание или среднее значение первого из двух признаков (X);
- хi= х1, х2, х3, … хn – реализации (даты или количественные значения) первого из двух признаков, получаемые в результате проведения опытов;
-  – математическое ожидание или среднее значение второго из двух признаков (Y);
– математическое ожидание или среднее значение второго из двух признаков (Y);
- уi= у1, у2, у3, … уn – реализации (даты или количественные значения) второго из двух признаков, получаемые в результате проведения опытов;
- n – численность каждой из совокупностей – количество учтенных в ней наблюдений, замеров;
- i – порядковый номер единицы учета в совокупности: i = 1… n.
Далее перечислены важнейшие свойства ковариации как статистической величины, которые обучающиеся исследуют в ходе выполнения лабораторной работы.
1. Коварианса (количественная оценка ковариации) может приобретать как положительные, так и отрицательные значения. В зависимости от этого в первом случае ковариация признается положительной, а во втором – отрицательной. При положительной ковариации с ростом значений первой переменной (X) значения второй переменной (Y) также увеличиваются. При отрицательной ковариации с ростом значений первой переменной (X) значения второй переменной (Y) уменьшаются. При этом следует учитывать, что если переменные величины X и Y являются независимыми случайными величинами, то ковариация между ними отсутствует, и коэффициент ковариации равен 0. Такие величины, имеющие нулевую ковариацию, называют некоррелированными. Независимые случайные величины всегда некоррелированы, но не наоборот.
2. Также следует иметь в виду, что только по абсолютному значению ковариации нельзя судить о тесноте связи между рассматриваемыми случайными величинами (X и Y). Это обусловлено тем, что её масштаб зависит от их дисперсий. Однако преодолеть указанную проблему удается путем деления значения ковариации на произведение среднеквадратических отклонений исследуемых в ковариационном анализе переменных. В следствие таких преобразований мы получим парный коэффициент корреляции Пирсона, поскольку коварианса интегрирована в его структуру в следующем порядке:

где:
- r(X;Y) – парный коэффициент корреляции между переменными X и Y;
- X – одна из двух переменных, взаимосвязанная с неким признаком Y;
- Y – одна из двух переменных, взаимосвязанная с неким признаком X;
- Cov(X;Y) – оценка ковариации переменных величин X и Y.
Оценка парного коэффициента корреляции (rXY) уже не зависит от величины дисперсии каждого из коррелирующих признаков. Свойства парного коэффициента корреляции и сферы его применения рассмотрены нами ранее. Кроме того, поскольку коэффициент ковариации есть величина размерная, интерпретировать результаты его вычисления оказывается затруднительно. Это вносит некоторые ограничения на область применения ковариационного анализа, особенно если сравниваются разноразмерные величины. Применение парного коэффициента корреляции, выраженного в безразмерных единицах измерения, позволяет преодолеть и эту проблему.
3. Связь между ковариацией и дисперсией становится понятной если принять во внимание, что ковариация случайной величины (X) с самой собой (X) является её дисперсией или средним квадратом отклонений. Это легко подтвердить, преобразовав соответствующим образом базовую формулу для вычисления значений коэффициента ковариации:

Здесь:
- σ2Х – дисперсия или средний квадрат отклонений переменной Х;
- DX – дисперсия или средний квадрат отклонений переменной Х;
- CovXX – оценка ковариации признака с самим собой (переменной X и переменной X);
- 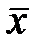 – математическое ожидание или среднее значение признака (X);
– математическое ожидание или среднее значение признака (X);
- хi= х1, х2, х3, … хn – реализации (даты или количественные значения) первого из двух признаков, получаемые в результате проведения опытов;
- n – численность совокупности – количество учтенных в ней наблюдений, замеров;
- i – порядковый номер единицы учета в совокупности: i = 1… n.
4. Соотношение между оценками ковариации и дисперсии можно трактовать несколько шире, например, ковариация между переменными X и Y в случае наличия между ними линейной функциональной зависимости, описываемой уравнением вида y = ax + b, равна корню квадратному из произведения их дисперсий:
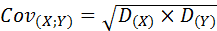 , при условии Y = aX + b,
, при условии Y = aX + b,
где:
- Cov(X;Y) – оценка ковариации двух признаков или коэффициент ковариации двух переменных величин X и Y;
- D(X) – дисперсия или средний квадрат отклонений переменной Х;
- D(Y ) – дисперсия или средний квадрат отклонений переменной Y;
- X – одна из двух переменных, взаимосвязанная с неким признаком Y;
- Y – одна из двух переменных, взаимосвязанная с неким признаком X;
5. Максимальным пределом (абсолютным максимумом или лимитом значений) коэффициента ковариации выступает корень квадратный из произведения их дисперсий:
 ,
,
где:
- Cov(X;Y) – оценка ковариации двух признаков или коэффициент ковариации двух переменных величин X и Y;
- D(X) – дисперсия или средний квадрат отклонений переменной Х;
- D(Y) – дисперсия или средний квадрат отклонений переменной Y;
- X – одна из двух переменных, взаимосвязанная с неким признаком Y;
- Y – одна из двух переменных, взаимосвязанная с неким признаком X.
6. Средний квадрат отклонений (дисперсия) суммы (или разности) двух случайных величин X и Y равен сумме их дисперсий плюс (или соответственно, минус) удвоенное значение коэффициента ковариации между ними:
 ,
,
или, соответственно:
 .
.
7. Постоянный множитель (a), если таковой присутствует в структуре алгоритма вычисления коэффициента ковариации, можно выносить за знак ковариации:
 =
=  =
= 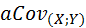
8. Ковариация не изменится если к одной из случайных величин, или к двум случайным величинам, прибавить некоторую постоянную величину (a) или, если к первой переменной прибавить одну постоянную величину (а), а ко второй – другую (b):
 =
=  =
= 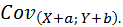
9. Учитывая два предыдущих свойства ковариации, можно утверждать, что:
 .
.
10. Также из анализа приведенных выше свойств ковариации можно сделать заключение о том, что ковариация двух переменных величин (признаков деревьев и кустарников или иных лесоводственных объектов), значения которых выражены в безразмерных нормированных единицах (как отношение текущего значения к соответствующему среднеквадратическому отклонению каждой из них) представляет собой парную корреляцию. В этом случае коэффициент ковариации, как и коэффициент корреляции, безразмерен, а по величине равен ему. Что бы убедиться в этом преобразуем рассмотренную выше формулу вычисления коэффициента корреляции через величину коэффициента ковариации.
 =
= 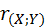
10. В математическом плане ковариация симметрична, в силу чего имеет место равенство:
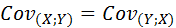 .
.
 2020-06-12
2020-06-12 133
133








