2020-06-08
323
Рассмотрим общий вид системы одновременных уравнений. Пусть 
–эндогенные переменные,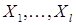 
– экзогенные переменные. Введем блочные матрицы 
и 
следующего вида:
.
Тогда общий вид системы одновременных уравнений записывается в матричной форме
,
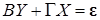где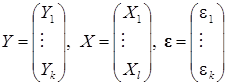 
.
Кроме регрессионных уравнений, называемых также поведенческимиуравнениями, модель может содержать тождества, которые представляют собой алгебраические соотношения между эндогенными переменными.
Например, для модели формирования спроса и предложения и цены равновесия имеем два поведенческих уравнения и тождество 
.
Тождества, вообще говоря, позволяют исключить некоторые эндогенные переменные и рассматривать систему регрессионных уравнений меньшей размерности. Так, в модели спроса и предложения можно положить 
ирассматривать структурную форму 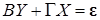, где
, 
.
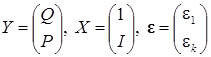Ограничимся рассмотрения случая двух уравнений с двумя эндогенными переменными, так как все необходимые аспекты теории можно проследить на этом простейшем случае. В то же время такое ограничение позволяет избежать излишней громоздкости в вычислениях.
Очевидно, что всегда можно выделить в левой части системы эндогенные переменные, т. е. записать уравнения в следующем виде:
Наборы переменных 
и 
могут быть произвольными. Параметры β, вообще говоря, векторные. Если применить к уравнениям системы обычный метод наименьших квадратов, то получатся несостоятельные оценки параметров α, β, γ. Таким образом, оценивание систем одновременных уравнений требует специальных методов.
