Модель спроса и предложения

До сих пор мы предполагали, что в регрессионной модели

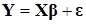
объясняющие переменные 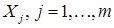,образующие матрицу 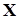, не являются случайными. Это означает, что при повторении серии выборочных наблюдений, значения переменных  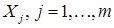 не изменяются, а значения  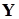изменяются за счет случайного члена 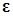. Подобное предположение, приводящее к значительным техническим упрощениям, может быть оправдано в том случае, когда экспериментальные данные представляют собой пространственную выборку.

В случае временного ряда, регрессоры которого представляют собой временной тренд, циклическую и сезонную компоненты, объясняющие переменные уже, очевидно, не случайны, т. е. наблюдения 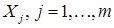 являются случайными величинами. В этом случае естественно возникает вопрос о коррелированности между регрессорами и ошибками регрессии 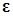. От этого существенно зависят результаты оценивания, причем не только количественно, но и качественно.

Одной из причин коррелированности регрессоров со случайными членами могут служить факторы, действующие одновременно и на сами регрессоры, и на объясняемые переменные при фиксированных значениях регрессоров. Иными словами, в рассматриваемой экономической ситуации значения объясняемых переменных и регрессоров формируются одновременно под воздействием некоторых внешних факторов. Это означает, что рассматриваемая модель не полна: ее следует дополнить уравнениями, в которых объясняемыми переменными выступали бы сами регрессоры. Таким образом, мы приходим к необходимости рассматривать системы одновременныхили регрессионных уравнений.

Классическим примером является одновременное формирование спроса   и предложения   товара в зависимости от его цены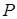

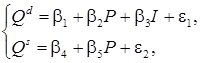
где 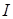– доход.

Если предположить, что рынок находится в состоянии равновесия, то в этих равенствах следует положить . В этом случае наблюдаемое значение 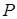– это цена равновесия, которая формируется одновременно со спросом и предложением.

Таким образом, 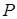 и 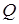 являются объясняемымипеременными, а величина дохода 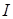– объясняющейпеременной. Разделение ролей между переменными в системе одновременных уравнений может быть проинтерпретировано следующим образом: переменные  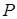и 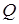    формируют свои значения, подчиняясь записанным уравнениям, т. е. внутри модели. Такие переменные называются эндогенными.Между тем переменная  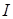считается в этих уравнениях заданной, ее значения формируются  вне модели. Такие переменные называются экзогенными.

С математической точки зрения, главное отличие между экзогенными и эндогенными переменными заключается в том, что экзогенные переменные не коррелируют с ошибками регрессии,между тем как эндогенные могут коррелировать (и, как правило, коррелируют). Естественно предположить, что схожие случайные факторы действуют как на цену равновесия, так и на спрос на товар. Причинная зависимость между переменными и приводит, очевидно, к коррелированности их со случайными членами. Набор экзогенных переменных может быть различным. Так, например, в модели спроса и предложения в качестве экзогенных переменных к доходу могут быть добавлены процентная ставка, временной тренд и т. д.