2020-06-12
295
В данном подразделе рассматриваются примеры решения некоторых задач по теории надежности. Кроме рассмотренных здесь примеров, рекомендуется пользоваться анализом методов решения задач, содержащимся в [2, 3, 6].
Пример 1. В энергосистеме имеется группа из n однотипных котлов, работающих в одинаковых условиях. Вероятность исправного состояния котла - p, а неисправного q=1-p. Найти вероятность рабочего состояния m котлов из n.
m = 4; n = 5; p = 0.98; q = 1 - 0.98 = 0.02.
Задача решается с применением схемы Бернулли.
Вероятность одновременного повреждения всех котлов - qn;
вероятность отказа всех котлов, кроме одного - npqn-1;
....................................................................................................
вероятность того, что в работе окажется m котлов изn - Cmn pm qn-m,
где Cmn= (n!)/[! (n-m)!] - число сочетаний из n элементов по n;
вероятность того, что в работе будут все котлы, кроме одного, - npn-1q;
вероятность того, что все котлы в рабочем состоянии - pn.
Сумма вероятностей всех возможных состояний соответствует разложению по биному Ньютона и равна единице.
|
|
|
Для числовых значений примера:
p = 5 x 0.984 x 0.02 = 0.0923, то есть вероятность рабочего состояния четырех котлов из 5 составляет 0.0923.
Пример 2. Статистическая вероятность повреждения любой фазы трехфазной линии составляет 0.01. Если повреждение одной фазы произошло, то повреждение любой другой фазы имеет статистическую вероятность 0.2, третья фаза при условии повреждения двух других повреждается с вероятностью 0.5. Найти соотношение вероятностей одно-, двух- и трехфазных повреждений при условии, что авария начинается с повреждения одной фазы.
Однофазные повреждения происходят с вероятностью 0.01 по условиям задачи. Вероятность двухфазных повреждений считается по формуле условной вероятности:
Р(АВ) = Рв(А) ´ Р(В) = 0.2´0.01 = 0.002;
Вероятность трехфазных повреждений:
Р(АВС) = Р(АВ) ´ Р(С) = 0.002 ´ 0.5 = 0.001.
Таким образом, соотношение вероятностей одно-, двух- и трехфазных повреждений трехфазной линии составляет 0.01: 0.002: 0.001 или 10: 2: 1.
Пример 3. Топливо на котельную подается по двум ниткам трубопровода. По каждой из ниток котельная может получить 50 % топлива для ее нормальной работы. Вероятность выхода из строя одной нитки трубопровода составляет 0.05. Какова вероятность сохранения рабочего состояния котельной?
Так как по каждой нитке трубопровода передается только половина необходимого количества топлива для нормальной работы котельной, отказ любой из двух ниток приводит к отказу работы котельной.
Вероятность выхода из строя хотя бы одной из двух ниток трубопровода составляет
q = q1 ´ p2 = 0.05 ´ (1 -0.05) = 0.0475.
Вторая нитка трубопровода выходит из строя с той же вероятностью.
|
|
|
Вероятность отказа составляет 2 х 0.0475 = 0.095.
Вероятность сохранения рабочего состояния котельной составит
р = 1 - 0.095 = 0.905.
Пример 4. Среднее значение времени наработки на отказ изделия составляет 12000 ч. Считаем, что отклонение от среднего значения для наработки на отказ подчиняется нормальному закону распределения с дисперсией 250000 ч2. Найти вероятность того, что для некоторого испытуемого изделия наработка на отказ будет находиться в пределах 12500... 13000 ч.
Вероятность того, что величина t будет находиться в пределах t 1< t < t2 находится по выражению:
Р(t1<t<t2) = 0.5{ Ф [(t2 - a) /s]} - 0.5 { Ф [(t1 - a) / s]} = 0.5 Ф [(13000-12000)/Ö250000] - - 0.5 Ф [(12500-12000)/Ö250000] = 0.5 Ф (2) - 0.5 Ф (1) = 0.4772 - 0.3411= 0.1361,
где t2 - верхний предел заданного диапазона;
t1 - нижний предел заданного диапазона;
a - математическое ожидание случайной величины;
s = ÖD - среднеквадратическое отклонение случайной величины t;
D - дисперсия;
Ф (x) - табулированный интеграл нормального распределения [1...5].
В данной работе интеграл вероятностей Ф (х) представлен в несколько приближенном виде на рис.5.
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5
Значения функции интеграла вероятностей Ф(х) для нормального закона распределения
Пример 5. Определить вероятность повреждения энергоблока, представляющего собой последовательное соединение парового котла, паровой турбины и электрического генератора. Паровая турбина получает весь пар от котла. Генератор расположен на одном валу с турбиной, то есть использует всю ее мощность. Вероятность повреждения отдельных элементов: котла qк = 0.02; турбины qт = 0.01; генератора qг = 0.001.
Энергоблок представляет из себя систему из трех последовательно соединенных элементов, то есть аварийный выход из работы хотя бы одного элемента приводит к отказу энергоблока.
Вероятности безотказной работы отдельных блоков составляют соответственно
рк = 1 - q к = 1 - 0.02 = 0.98;
рт = 1 - qт = 1 - 0.01 = 0.99;
рг = 1 - q г = 1 - 0.001 = 0.999.
Можно решить эту задачу анализом всех возможных сочетаний повреждения элементов блока. Всего их семь: 1) котла; 2) турбины; 3) генератора; 4) котла и турбины; 5) котла и генератора; 6) турбины и генератора; 7) котла, турбины и генератора.
При этом соответствующие вероятности отказа энергоблока в этих ситуациях составят:
q1 = 0.02 x 0.99 x 0.999 = 0.198;
q2 = 0.98 x 0.01 x 0.999 = 0.0098;
q3 = 0.98 x 0.99 x 0.001 = 0.001;
q4 = 0.02 x 0.01 x 0.999 = 0.0002,
q5, q6 и q7 практически равны 0.
Вероятность отказа энергоблока равна сумме вероятностей отказов элементов в этих семи ситуациях.
|
|
|
qэб = 0.0198 + 0.0098 + 0.001 + 0.0002 = 0.0308.
Задача может быть решена и более простым способом.
Вероятность безотказной работы энергоблока равна произведению вероятностей безотказной работы отдельных элементов:
рэб = 0.98 х 0.99 х 0.999 = 0.9692.
Вероятность отказа:
qэб =1 - рэб = 1 - 0.9692 = 0.0308.
Пример 6. Найти наименьшее число испытаний, при котором со статистической вероятностью b = 0.99 разность относительной частоты и вероятности отказа не превышает e £ 0.01. Статистические значения вероятности отказа и безотказной работы соответственно равны q = 0.02; p = 0.98. Распределение случайной величины статистической вероятности b считать нормальным.
Если известна статистическая вероятность отклонения частоты и вероятности отказа b, то по таблице интеграла вероятностей или приближенно по рис.5 следует найти х из:
Ф(х) = b, то есть при b = 0.99 х = 2.58.
Далее по формуле [2]:
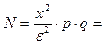2,582 x 0.98 x 0.02/0.012=1305.
Аналогично с помощью таблицы интеграла вероятностей или приближенно построенных графиков решаются и две обратные задачи
1. Нахождение статистической вероятности b отклонения вероятности отказа от его относительной частоты при известных e и N: находится величина х
,
а затем по таблице интеграла вероятностей находится Ф(х)= b.
2. Нахождение максимального отклонения относительной частоты отказов от заданной вероятности (e) при известных b и N.
Сначала по таблице интеграла вероятностей находят х как в прямой задаче, а затем находят e по формуле:
.
Пример 7. В течение пяти месяцев объем электропотребления завода (W) и число отключений в системе автоматики (N) имели следующие значения:
Месяцы
1 2 3 4 5
W, тыс.кВт.ч 1455 1380 1500 1390 1440
N, шт. 6 5 8 6 7
Найти коэффициент корреляции между W и N, составить уравнение регрессии между ними. Определить (если это допустимо) возможное число отключений, если план электропотребления на некоторый месяц определен 1450 тыс.кВт.ч.
Определим математические ожидания и среднеквадратические отклонения переменных W и N.
|
|
|
MW = (1455 + 1380 + 1500 + 1390 + 1440)/5 = 1433, тыс.кВт.ч;
MN = (6 + 5 + 8 + 6 + 7)/5 = 6.4, шт.
sW={ [(1455-1433)2+(1380-1433)2+(1500-1433)2+(1390-1433)2+(1440-1433)2]/4}0.5 =
49.19, тыс. кВт. ч;
аналогично sN = 1.14, шт.
Следует обратить внимание, что сумма квадратов отклонений делится по условию применения оценки среднеквадратического отклонения, то есть не на 5, а на 4, что связано с явной малостью объема выборки [2].
Коэффициент корреляции:
rWN= [(1455-1433)(6-6.4)+(1380-1433)(5-6.4)+(1500-1433)(8-6.4)+(1390-1433) x
x (6-6.4)+(1440-1433)(7-6.4)]/(4 x 49.19 x 1.14) = 0.865.
Снова используем оценку коэффициента корреляции, то есть делим на n -1=4, а не на n =5.
Уравнение регрессии:
N = rWN (sN /sW)(W - MW) + MN = 0.0205 W - 22.33, шт.
Коэффициент корреляции составляет 0.865, то есть достаточно высок, поэтому при заданном плане электропотребления 1450 тыс. кВт. ч, значение которого входит в интервал изменения величины W, допустимо определить возможное число отключений N:
N = 0.0205 x 1450 - 22.33 = 6.74, шт.
Литература
1. ГОСТ 27.002-89. Надежность в технике. Термины и определения.
2. Вентцель Е.С. Теория вероятностей. М., Наука, 1984.
3. Гук Ю.Б. Теория надежности в электроэнергетике, Л., Энергоатомиздат, 1990.
4. Надежность технических систем // Ю.К.Беляев, В.А.Богатырев, В.В.Болотин, И.А.Ушаков. М., Радио и связь, 1985.
5. Молчанов Ю.С. Надежность систем управления. М., Высшая школа, 1987.
6. Сборник задач и упражнений по теории надежности// под ред. В.В.Болотина., Радио и связь, 1983.
