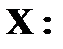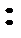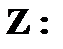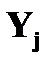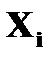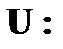|
| 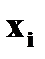
| 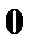
| 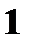
| 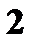
|
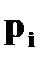
| 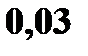
| 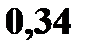
| 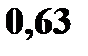
|
Математические операции над дискретными случайными величинами.
Пусть заданы две дискретные величины своими рядами распределения:
|
| 
| 
| 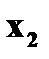
| 
| 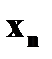
|
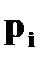
| 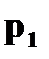
| 
| 
| 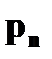
|
|
| 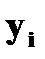
| 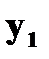
| 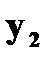
| 
| 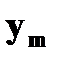
|
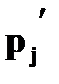
| 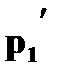
| 
| 
| 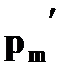
|
Произведением kX случайной величины X на постоянную k назовем случайную величину, которая принимает значения 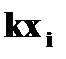 с теми же вероятностями
с теми же вероятностями 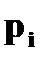
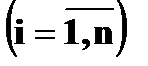 .
.
Определение. m – ой степенью случайной величины 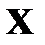 , то есть
, то есть 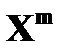 , назовем случайную величину, которая принимает значения
, назовем случайную величину, которая принимает значения 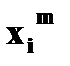 с теми же вероятностями
с теми же вероятностями 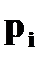
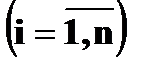 .
.
Пример. Дана случайная величина
|
| 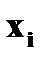
| 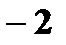
| 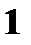
| 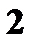
|
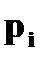
| 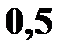
| 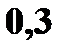
| 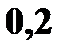
|
Найти закон распределения а) 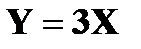 ; б)
; б) 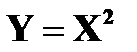 .
.
Решение. а) Значения 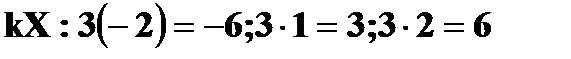 . Вероятности те же.
. Вероятности те же.
|
| 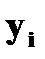
| 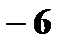
| 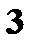
| 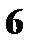
|
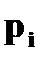
| 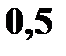
| 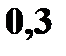
| 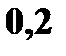
|
б) Значения случайной величины 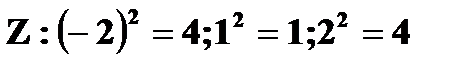 с теми же вероятностями. Случайная величина
с теми же вероятностями. Случайная величина 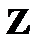 имеет два различных значения 1 и 4. Так как 4 можно получить, как -
имеет два различных значения 1 и 4. Так как 4 можно получить, как - 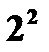 , так и
, так и 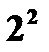 , то по теореме сложения вероятностей
, то по теореме сложения вероятностей 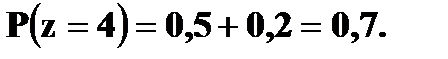 Итак, закон распределения случайной величины
Итак, закон распределения случайной величины
|
| 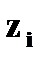
| 
| 
|
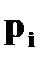
| 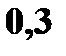
| 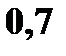
|
Пусть закон распределения случайной величины 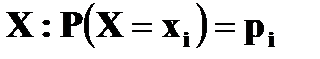
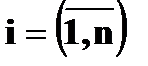 , а случайной величины
, а случайной величины 
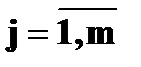 .
.
Определение. Случайные величины X и Y называются независимыми, если выполняется соотношение
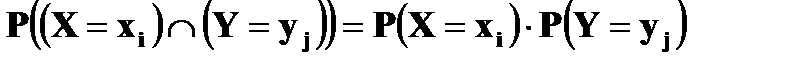 , для всех
, для всех 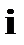 и
и  , где
, где 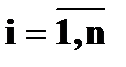 , а
, а 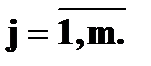
Суммой (разностью, произведением) случайных величин X и Y назовем случайную величину, которая принимает все возможные значения
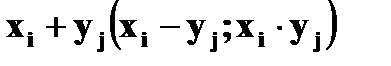 ,
,
где 
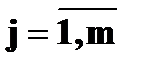 , с вероятностями
, с вероятностями 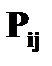 того, что случайная величина
того, что случайная величина 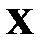 примет значение
примет значение 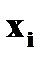 , а случайная величина
, а случайная величина 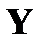 примет значение
примет значение  .
.
Пример. Даны законы распределения случайных величин
|
| 
| 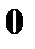
| 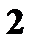
| 
|
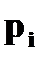
| 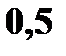
| 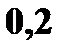
| 
|
|
| 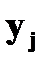
| 
| 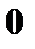
| 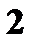
|
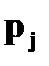
| 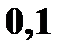
| 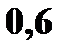
| 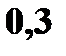
|
Найти законы распределения случайных величин а) 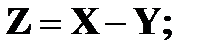
б) 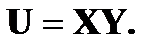
Для удобства подсчета составим таблицу
|
| 
| 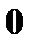
| 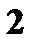
| |
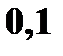
| 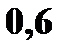
| 
| ||
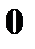
| 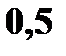
|  0,05
0,05
|  0,30
0,30
| 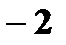 0,15
0,15
|

| 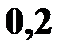
|  0,02
0,02
|  0,12
0,12
| 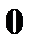 0,06
0,06
|

| 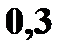
| 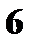 0,03
0,03
|  0,18
0,18
| 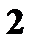 0,09
0,09
|
Например, X = 2 (второй элемент первого столбца), а Y = 0 (второй элемент первой строки). На пересечении строки и столбца стоит соответствующий элемент 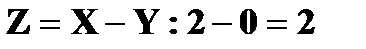 с вероятностью
с вероятностью  С учетом того, что среди 9 возможных значений
С учетом того, что среди 9 возможных значений  есть одинаковые, получим закон распределения
есть одинаковые, получим закон распределения
| Z: | 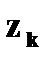
| 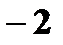
| 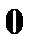
| 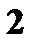
| 
| 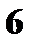
|
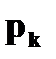
| 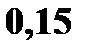
| 
| 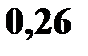
| 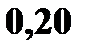
| 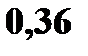
|
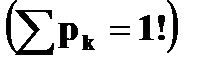
б) Аналогично получается закон распределения 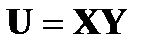
|
| 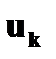
| 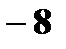
| 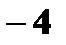
| 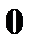
| 
| 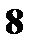
|
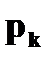
| 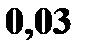
| 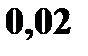
| 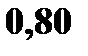
| 
| 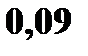
|
Числовые характеристики случайных величин
 2020-06-08
2020-06-08 96
96