Непрерывные случайные величины. Плотность вероятности

Определение. Плотностью вероятности (плотностью распределения или просто плотностью) f(x) непрерывной случайной величины 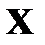называют производную ее функции распределения, то есть

График плотности вероятности называют кривой распределения.

Свойства плотности:

2. Вероятность попадания случайной величины в интервал равна

3.Функция распределения выражается через плотность

Геометрическая интерпретация свойств 2 и 3:

Первое свойство означает, что кривая распределения лежит не ниже оси x, а свойство 4 – полная площадь фигуры, ограниченной кривой распределения и осью 0x равна 1.

Для непрерывной случайной величины числовые характеристики имеют вид:

(если интегралы сходятся).

Пример. Функция f(x) задана в виде:

Найдите: a) значение постоянной А, при которой функция будет плотностью вероятности некоторой случайной величины X;

б) выражение функции распределения F(x);

в) вычислите вероятность того, что случайная величина X примет значения на отрезке ;

г) найдите математическое ожидание и дисперсию случайной величины X.

Решение.

а) Чтобы f(x) была плотностью вероятности некоторой случайной величины X, она должна быть неотрицательной и

Следовательно,

Имеем тогда

б) Если то

Если X > 1, то

Получаем, что

в)

г)

Некоторые законы распределения

Биноминальный закон распределения

Дискретная случайная величина X принимает значения с вероятностями, которые подсчитываются по формуле Бернулли , где n – общее число испытаний; p – вероятность успеха в каждом испытании; q – вероятность наступления неудачи. Так что