Математическим ожиданием или средним значением дискретной случайной величины 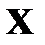 (обозначается
(обозначается  ) назовем сумму произведений всех ее значений на соответствующие им вероятности.
) назовем сумму произведений всех ее значений на соответствующие им вероятности.

 , если значений счетное число.
, если значений счетное число.
Пример. Вычислить MX в задаче 1.
Решение. 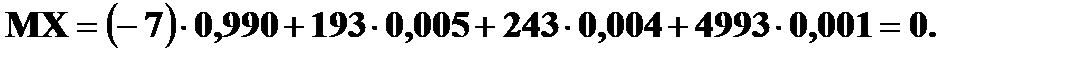 Полученный результат означает, что все вырученные деньги от продажи билетов лотереи идут на выигрыши.
Полученный результат означает, что все вырученные деньги от продажи билетов лотереи идут на выигрыши.
Замечание. Так как дискретная случайная величина может принимать счетное число значений, то ряд 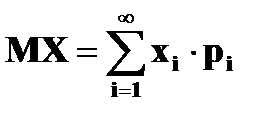 может расходиться. Тогда случайная величина не имеет конечного математического ожидания.
может расходиться. Тогда случайная величина не имеет конечного математического ожидания.
Свойства математического ожидания:
Предположим, что MX и MY – конечны.
1. 

2. 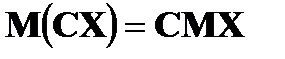
3. 
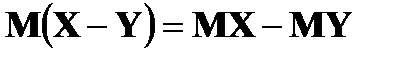
4. 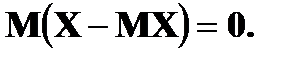
Пример. Известно, что 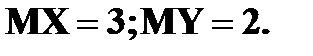 Найдите
Найдите  где
где 
Решение. Используя свойства 2, 3, 6, 1, имеем

Дисперсия
Дисперсией DX случайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидания, то есть 
Если 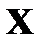 – дискретная случайная величина и
– дискретная случайная величина и 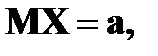 то
то 
Средним квадратическим отклонением (стандартным отклонением или стандартом)  случайной величины
случайной величины  называется арифметическое значение корня квадратного из ее дисперсии.
называется арифметическое значение корня квадратного из ее дисперсии.

Свойства дисперсии:
1.  , где
, где  – постоянная;
– постоянная;
2. 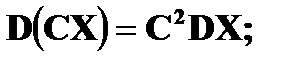
3. 
4. Если 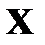 и
и  — независимые случайные величины, то
— независимые случайные величины, то 
Пример. 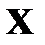 и
и  — независимые случайные величины.
— независимые случайные величины. 
Найти  .
.
Решение. По свойствам 4, 2

Функция распределения случайной величины.
Определение. Функцией распределения случайной величины 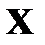 назовем функцию
назовем функцию  , выражающую для любого
, выражающую для любого 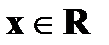 вероятность того, что случайная величина
вероятность того, что случайная величина  примет значения, меньше
примет значения, меньше  :
:  (X< x).
(X< x).
Геометрически: функция распределения  – это вероятность попасть случайной величине
– это вероятность попасть случайной величине 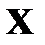 левее заданной точки
левее заданной точки 

Пример. Дан ряд распределения случайной величины
| | 
| 
| 
| 
| 
|

| 
| 
| 
| 
|
Найти и изобразить графически ее функцию распределения.
Решение.
1. x ≤ 1 F(x) = 0 ( в том числе и для x = 1, так как F(1) = P(X<1))
2. 1 < x ≤ 4 F(x) = P(X = 1) = 0, 4 (в том числе и для x = 4)
3. 4 < x ≤ 5 F(x) = P(X = 1) + P(X = 4) = 0, 5 (в том числе и для x = 5)
4. 5 < x ≤ 7 F(x) = P(X = 1) + P(X = 4) + P(X = 5) = 0, 5 + 0, 3 = 0,8
5. x > 7 F(x) = P(X = 1) + P(X = 4) + P(X=5) + P(X = 7) = 0,8 + 0,2 =1
Итак, 

Заметим, что при переходе слева к точкам разрыва функция F(x) сохраняет свои значения, то есть F(x) – непрерывна слева.
Из графика видно, что F(x) – разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений.
Сумма всех скачков функции распределения равна 1.
Свойства функции распределения:
1. 0 ≤ F(x) ≤ 1
2. Функция распределения F(x) есть неубывающая функция на всей числовой прямой.
3.  lim
lim  ,
,  lim
lim  =1
=1


4. Вероятность попадания случайной величины  в интервал
в интервал  равна приращению ее функции распределения, то есть
равна приращению ее функции распределения, то есть 
Пример. Функция распределения

Найти 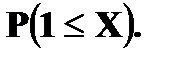
Решение. P(1 ≤ X < 3) = 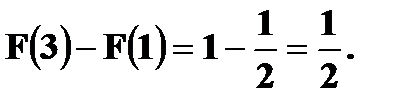
 2020-06-08
2020-06-08 88
88









