Прием преобразования условия (синтетический)

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное

Образовательное учреждение  высшего образования

«ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

 

Факультет физико-математических и естественных наук

Кафедра «Информатика и методика обучения информатике и математике»

 

 

Направление подготовки   Профиль

44.03.01 «Педагогическое образование» «Математика»

 

 

Контрольная работа по

МЕТОДИКЕ ОБУЧЕНИЯ И ВОСПИТАНИЯ (МАТЕМАТИКА)

               

                    

        

Выполнил: студент гр. 17 ЗФПМ51

Кальманова А.М.

                                         Методист: Марина Е.В.

----------------------------------------------------------------

(оценка, подпись)

Пенза 2020 г.

2 вариант

Задание 1. Проанализируйте понятийный аппарат темы «Четырехугольники», раскрыв понятие как форму мышления (содержание, объем, определение, классификация понятия).

Тема «Четырехугольники» (Геометрия 7-9 классы, Атанасян Л.С.) включает в себя следующие параграфы:

 - многоугольники;

 - параллелограмм и трапеция;

 - прямоугольник, ромб, квадрат.

Первый параграф «Многоугольники» состоит из пунктов: 1) многоугольник; 2) выпуклый многоугольник; 3) четырехугольник.

Во второй параграф «Параллелограмм и трапеция» входят следующие пункты: 1) параллелограмм; 2) признаки параллелограмма; 3) трапеция.

Третий параграф «Прямоугольник, ромб, квадрат» содержит пункты: 1) прямоугольник; 2) ромб и квадрат; 3) осевая и центральная симметрии.

Для проведения анализа понятийного аппарата темы «Четырехугольники» выделим компоненты для основных понятий:

· Содержание и объем;

· Определение вида определения;

· Структура определения

· Классификация понятий;

При классификации всех четырехугольников за основание классификации принимается сначала взаимное расположение противоположных сторон – не параллельность или параллельность их, вследствие чего множество всех выпуклых четырехугольников разбивается на три класса:

· четырехугольники, не имеющие параллельных сторон;

· трапеции (одна пара параллельных сторон);

· параллелограммы (две пары параллельных сторон).

 

За основание классификации параллелограммов принимается равенство или неравенство смежных сторон (собственно параллелограммы и ромбы), а также отсутствие или наличие прямого угла (собственно параллелограммы и прямоугольники).

В основу классификации ромбов кладется отсутствие или наличие прямого угла (собственно ромбы и квадраты).

При классификации прямоугольников за основание принимается равенство или неравенство смежных сторон (собственно прямоугольники и квадраты).

Классификация трапеции проводится сначала по длине боковых сторон (равнобедренная и неравнобедренная трапеции); затем неравнобедренные трапеции в свою очередь разбиваются на прямоугольные и непрямоугольные.

 

 

                            Четырехугольники

              Параллелограмм     Трапеция

          Прямоугольник    Ромб

                    Квадрат

 

Определение многоугольника. Фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а не смежные отрезки не имеют общих точек, называется многоугольником. Существенные признаки: 1) геометрическая фигура; 2) состоит из отрезков; 3) смежные отрезки не лежат на одной прямой; 4) не смежные отрезки не имеют общих точек. Структура определения – импликативная, признаки связаны отношением следования.

Содержание понятия – все фигуры, в которых смежные отрезки не лежат на одной прямой, а смежные отрезки не имеют не имеют общих точек.

Объем понятия – множество всех фигур, составленных из отрезков.

Выпуклый многоугольник. Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Содержание понятия – все многоугольники, если они лежат по одну от прямой, проходящей через две соседние вершины.

Объем понятия – множество всех многоугольников.

Определение параллелограмма. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. Структура определения - конъюктивная: признаки соединены союзом «и».

Содержание понятия  - все многоугольники, у которых противоположные стороны попарно параллельны.

Объем понятия – множество всех параллелограммов.

Определение параллелограмма дается через род и видовое отличие (род – четырехугольник, видовое отличие − противоположные стороны попарно параллельны)

Определение трапеции. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Структура понятия – конъюктивная: признаки соединены союзом «и».

Содержание понятия – все многоугольники, у которых две стороны параллельны, а две другие стороны не параллельны.

Объем понятия – множество всех трапеций.

Определение трапеции дается через род и видовое отличие (род – четырехугольник, видовое отличие − две стороны параллельны, другие две не параллельны).

Определение прямоугольника. Прямоугольником называется параллелограмм, у которого все углы прямые. Структура понятия – конъюктивная: признаки соединены союзом «и».

Содержание понятия – все многоугольники, у которых все углы прямые.

Объем понятия – множество всех прямоугольников.

Определение прямоугольника дается через род и видовое отличие (род – параллелограмм, видовое отличие − углы прямые).

Определение ромба. Ромбом называется параллелограмм, у которого все стороны равны. Структура понятия – конъюктивная, поскольку признаки соединены союзом «и».

Содержание понятия – все многоугольники, у которых все стороны равны, диагонали взаимоперпендикулярны.

Объем понятия – все множество ромбов.

Определение ромба дается через род и видовое отличие (род –параллелограмм, видовое отличие − стороны равны).

Определение квадрата. Квадратом называется прямоугольник, у которого все стороны равны. Структура понятия – конъюктивная, поскольку признаки соединены союзом «и».

Содержание понятия – все многоугольники, у которых все стороны равны, все углы прямые.

Объем определение – все множество квадратов.

Определение квадрата дается через род и видовое отличие (род – прямоугольник, видовое отличие − стороны равны).

Задание 2. Рассмотрите различные приемы раскрытия содержания теоремы. Приведите примеры.

Основными видами математических суждений являются аксиомы и теоремы. Суждение – форма мышления, в которой что-либо утверждается или отрицается о существовании предметов, связях между предметом и его свойствами или об отношениях между предметами.

Аксиома – это суждение, принимаемое без доказательства в данной теории.

Теорема – это суждение, истинность которого устанавливается посредством доказательства.

В формулировке каждой теоремы указывается, при каких условиях рассматривается математический объект или отношение объектов и что об этом объекте или отношении объектов утверждается. Поэтому теоремы часто формулируются в виде условных предложений: если А, то В (такая форма теоремы называется условной или импликативной). Иногда теоремы формулируются в форме утвердительных предложений (Вертикальные углы равны. Сумма смежных углов равна 180°). Такая форма называется категорической. Некоторые теоремы формулируются в разделительной дизъюнктивной форме: А есть или В, или С, или Д.

Примеры: 1) Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны. 2) При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.

Рассмотрим теорему: А=> В. Назовем её прямой теоремой. Из неё можно построить следующие предложения:

1) Обратное: В=>А

2) Противоположное: А =>В

3) Обратное противоположному: В => А

Пример: Теорема Пифагора: Рассмотрим треугольник АВС, (∟В=90°=>АС²=АВ²+ВС)

Чтобы получить формулировку обратной теоремы, надо оставить без изменения разъяснительную часть исходной теоремы, а условие и заключение поменять местами: 1) Теорема обратная теореме Пифагора: Рассмотрим треугольник АВС: (АС²=АВ²+ВС=>∟В=90°)

Теорему, противоположную исходной, можно получить, если разъяснительную часть оставить без изменения, а условие и заключение заменить их отрицаниями.

Условие всякой теоремы является достаточным условием по отношению к заключению. В свою очередь заключение – это необходимое условие по отношению к условию этой теоремы.

Способ связи аргументов от условия к заключению суждения называют методом доказательства. Методы доказательства делят на прямые и косвенные. Различают приемы прямого доказательства: прием преобразования условия суждения (синтетический); прием преобразования заключения суждения (восходящий анализ); отыскание необходимых признаков справедливости суждения с последующей проверкой обратимости рассуждений (нисходящий анализ); прием последовательного преобразования то условия, то заключения суждения. К приемам косвенного доказательства относят: 1) метод доказательства от противного (истинность доказываемого утверждения устанавливается посредством опровержении противоречащего ему суждения); 2) разделительный (доказываемое утверждение рассматривается как один из возможных вариантов предложений, когда все предположения отвергаются, кроме одного).

Прием преобразования условия (синтетический)

Доказательство математического утверждения называется синтетическим, если оно осуществляется по следующей логической схеме: P₁(x)_→P₂(x)_→P₃(x)_→…P_n-1(x)→P_n(x) = P(x), где Т – определенная совокупность предложений той математической теории, в рамках которой доказывается данное утверждение. Таким образом, при синтетическом методе доказательства теоремы цепочка силлогизмов строится так, что мысль движется от условия теоремы к ее заключению.

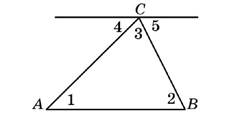Пример. Рассмотрим синтетическое доказательство теоремы «о сумме внутренних углов треугольника.»     

Дано: АВС – треугольник

Доказать:

Ð1+Ð2+Ð3=180°

                                                            

Доказательство:

 

1. «Рассмотрим треугольник АВС»

2. «Проведем через вершину В прямую, а, параллельную АВ.»

3. «Рассмотрим Ð1 и Ð4, как эти углы называются?»

«Правильно, они являются накрест лежащими углами при пересечении параллельных прямых а и АС и секущей АВ, а значит, Ð1=Ð4.»

4. «Теперь рассмотрим Ð3 и Ð5, что вы можете о них сказать?»

«Правильно, они накрест лежащие при пересечении параллельных прямых, а и АС и секущей ВС, а значит, Ð3=Ð5.»

5. «Посмотрите на углы 3,4 и 5, что можно про них сказать»

«Правильно, они образуют развернутый угол»

«Мы уже знаем, что сумма развернутого угла равно 180°, Ð4+Ð3+Ð5= 180°.»

6. «А так как Ð1=Ð4, а Ð3=Ð5,мы можем переписать наше выражение как Ð1+Ð2+Ð3=180°»

7. «Мы доказали, что сумма внутренних углов в треугольнике равна 180°»