Алгоритм решения линейного уравнения

1) Упростить при необходимости выражения, стоящие в левой и правой части уравнения. При необходимости привести подобные.

2) Перенести все члены уравнения, содержащие неизвестное, в левую часть, а члены уравнения, не содержащие неизвестного, в правую.

3) Привести подобные в левой части уравнения и выполнить арифметические действия с числами в правой части уравнения.

4) Разделить обе части уравнения на коэффициент при неизвестном, если он не равен нулю.

Пример

Решим уравнение: 2(х + 3) – 3(х + 2) = 5 – 4(х + 1)

Упростим уравнение, раскрыв скобки в левой и правой частях уравнения по правилам.

2х + 6 – 3х – 6 = 5 – 4х – 4

Приведём подобные.

(2х – 3х) + (6– 6) = (5 – 4) – 4х

– х = 1 – 4х

Перенесём член уравнения, содержащий неизвестное, из правой в левую часть, изменив при этом его знак.

– х + 4х = 1

Приведём подобные в левой части уравнения.

3х = 1

Разделим обе части уравнения на коэффициент при х, т.е. на 3.

х =

Мы нашли значение переменной. Значит, мы решили уравнение.

 

Рассмотренные уравнения содержат одну переменную. Они называются линейными уравнениями с одной переменной. Но в математике часто встречаются уравнения, содержащие две переменные. Это уравнения вида ax + by = c. Они так и называются: уравнения с двумя переменными.

Решением уравнения с двумя переменными x и y называется упорядоченная пара чисел (x;y), при подстановке которых в это уравнение получается верное числовое равенство.

Решениями уравнения ax + by = c, в случае, когда b≠0, являются пары , где х – любое число.

Если рассматривают два уравнения с двумя неизвестными, в которых неизвестные числа одни и те же, то их объединяют в систему и рассматривают совместно.

Например,

При решении систем уравнений используют различные методы.

Метод подстановки

1) Преобразовываем одно из уравнений системы таким образом, чтобы можно было выразить одну переменную через другую.

2) Подставляем полученное значение переменной в другое уравнение системы.

3) Решаем полученное линейное уравнение с одной переменной.

4) Полученное значение переменной подставляем в выражение, полученное на первом шаге.

5) Значения переменных и будут решениями системы.

 

Преобразуем уравнение . Получим: x + y = 6x + 4y. Далее: –3у=5х. Выразим у через х: у = .

Подставим полученное значение у во второе уравнение системы.

  5х + 3∙( =0

Решим полученное уравнение.

0=0. Значит, это уравнение верно при любом значении х. Данное решение говорит о том, что у исходной системы бесконечно много решений. Все их можно записать в виде пары (х; ).

Но не все системы имеют бесконечно много решений. Они могут иметь одно решение, бесконечно много решений или не иметь решений вовсе.

С помощью графического метода решения систем это можно понять более наглядно.

Графический метод

Графической иллюстрацией уравнения с двумя неизвестными является построение его графика на координатной плоскости. Зависимость у(х) – это прямая.

Таким образом, если мы на координатной плоскости построим графики обоих уравнений системы, то точки пересечения этих графиков и будут решениями системы.

Значит, если прямы пересекутся в одной точке, значит, у системы одно решение – пара (х;у). Если прямые не пересекаются (то есть они параллельны), значит, исходная система не имеет решений. Если же обе прямые полностью совпадут (наложатся друг на друга), то можно сделать вывод о бесконечном количестве решений системы.

Примеры

                                            

 

           

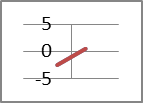
      1 решение: 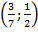                         нет решений              бесконечно много решений

Метод сложения

Ранее мы уже с вами узнали, что уравнения можно складывать друг с другом почленно. Это свойство можно использовать для решения систем уравнений с двумя неизвестными.

Если у обоих линейных уравнений коэффициенты при каком-нибудь неизвестном одинаковы или отличаются только знаком, систему можно решить методом алгебраического сложения, то есть сложить почленно каждую часть уравнений. Если это не так, то можно уравнять модули коэффициентов при каком-нибудь одном из неизвестных, умножая левую и правую части каждого уравнения на подходящие числа.

Решим две системы уравнений методом алгебраического сложения.

1)        

 

2)    

 

 

Свойства степеней

 

Степенью числа а с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а.

В выражении aⁿ число а называют основанием степени, число n называют показателем степени.

Вычисление значения степени называют действием возведения в степень.

7∙2⁴ - 5∙3² = 7∙16 - 5∙9 = 112 – 45 = 67

Свойства степеней

1. При умножении степеней с одинаковыми основаниями основание остаётся прежним, а показатели степеней складываются. a^m∙aⁿ = a^m+n

2. При делении степеней с одинаковыми основаниями основание остаётся прежним, а показатели степеней вычитаются. a^m : aⁿ = a^{m – n}, m>n, a≠0

3. При возведении степени в степень основание остаётся прежним, а показатели степеней перемножаются. (a^m)ⁿ = a^mn

4. При возведении в степень произведения в эту степень возводится каждый множитель. (ab)ⁿ = aⁿbⁿ

5. При возведении в степень дроби в эту степень возводятся числитель и знаменатель.  =

Пример