Если рассматривать геометрический смысл модуля, то говорят, что модуль – расстояние до конкретной точки координатной прямой от начала координат в единичных отрезках. Так как никакое расстояние не может быть отрицательным, то легко понять, что значение модуля любого числа – это число неотрицательное. Например, расстояние от начала координат до точки А(-5) равно 5. По-другому, |-5|=5.
Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчёта, т.е. удалена от начала координат на 0 единичных отрезков. Для положительного числа и нуля модуль равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули: |-а|=|а|.
Итак, 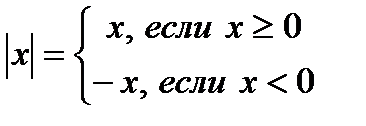 .
.
Свойства модулей чисел: 1) |а|≥0; 2) |ab|=|a|⸳|b|; 3) 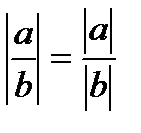 (b≠0); 4) |a2|=a2; 5) |a|=|-a|
(b≠0); 4) |a2|=a2; 5) |a|=|-a|
Решим уравнение |x-1|=2, используя определение и смысл модуля.
|-2|=2 и |2|=2. Т.е. х-1= –2 или х-1=2. Получили 2 линейных уравнения. Корнем уравнения х-1= –2 является число х= –1, а корнем уравнения х-1=2 является число х=3.
Проверим решения. |-1-1|=|-2|=2, |3-1|=|2|=2.
Перейдём к построению графика функции у= |х|. Вспомним алгоритм построения графика функции:
1) находим область определения функции;
2) берём несколько точек из области определения функции;
3) подставляем значения х из ООФ в уравнение функции;
4) полученные пары чисел (х;у) – точки графика функции.
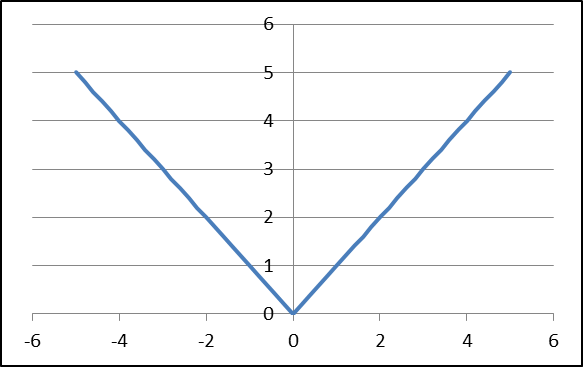
Областью определения функции «Модуль» является вся числовая ось. Для построения графика возьмём 3 или 5 точек. 1 точка – вершина графика, 2 или 4 точки – для более точного построения.
| х | -2 | -1 | 0 | 1 | 2 |
| у | 2 | 1 | 0 | 1 | 2 |
Построим график функции у=|х-1|. Так как в формулу функции входит модуль, то его необходимо раскрыть, рассмотрев 2 случая. Поэтому функцию можно записать в виде 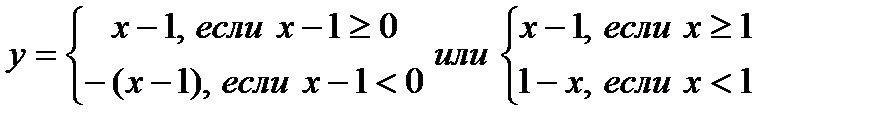
То есть при х≥1 строится луч, удовлетворяющий уравнению х-1, а при х<1 строится луч, удовлетворяющий уравнению 1-х.
Для построения графика возьмём точки, ближайшие к 1 – точки -1, 0, 1, 2 и 3.
|x-1|=|0-1|=1, |x-1|=|1-1|=0, |x-1|=|2-1|=1.
| х | -1 | 0 | 1 | 2 | 3 |
| у | 2 | 1 | 0 | 1 | 2 |
Центральная точка (вершина графика) – точка А(1;0), крайняя левая точка С (-1;2), крайняя правая точка В(3;2).
СА – луч 1-х, а ВА – луч х-1.
Таким образом, графиком данной функции является ломаная САВ.
Свойства графика функции «Модуль»:
1) область определения функции – вся числовая ось;
2) функция симметрична относительно вертикальной прямой, проходящей через вершину;
3) функция убывает при х 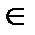 (-
(- 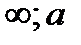 ), возрастает при х
), возрастает при х 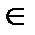 (-
(- 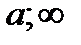 ), где а – координата вершины;
), где а – координата вершины;
4) функция ограничена снизу если у= |kx+b| и ограничена сверху, если у= – |kx+b|.
Используя определения арифметического квадратного корня и модуля, можно сделать вывод, что при любом значении х верно равенство 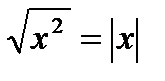 .
.
Кроме построения графиков функций, содержащих модуль, и решения уравнений модуль ещё рассматривается при решении неравенств, содержащих модуль.
Рассмотрим неравенство |х|≤а, где а>0. Этому неравенству удовлетворяют все точки х, находящиеся на расстоянии, не большем а, от точки 0, т.е. точки отрезка [-a;a].
Отрезок [-a;a] – это множество чисел х, удовлетворяющих неравенству -а≤х≤а.
Следовательно, неравенство |х|≤а, где а>0, означает то же самое, что и двойное неравенство -а≤х≤а.
Решим неравенство |5-3х|<8. Запишем данное неравенство в виде -8<5-3x<8.
-8<5-3x<8 → -8-5< -3x<8-5 → -13< -3x<3 → - 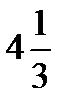 < -x<1 → 1< x <
< -x<1 → 1< x < 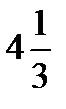 .
.
Решим ещё одно неравенство в качестве примера. |х-1|≥2.
Рассмотрим два случая: если х-1 ≥0 и если х-1<0.
Пусть х-1 ≥0. Тогда х-1≥2. Значит, х≥3. Пусть х-1<0, тогда –(х-1)≥2 или х-1≤ -2. Отсюда х≤ -1.
Итак, во-первых, неравенство |х-1|≥2 выполняется при х≥3, а во-вторых, при х≤ -1. Так как возможны оба этих случая, то эти решения объединяются.
Ответ: 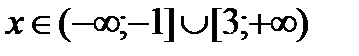 .
.
 2020-06-10
2020-06-10 2517
2517
