ООФ. ОЗФ. Определение свойств по графику. Построение графика по точкам

 

Ранее (в 6, 7 и начале 8 классов) вы познакомились с понятием функции, со свойствами и графиками некоторых функций и способами задания функций.

Если рассматривать графики реальных зависимостей, можно заметить, что всегда имеются две взаимосвязанные величины. С изменением первой величины меняются и значения второй. В таких ситуациях первую величину называют независимой, а другую зависимой. Так, например, с течением времени меняются рост человека, вес ребёнка, пройденная бегуном дистанция. В этих примерах время – независимая величина. Остальные величины, значения которых определяются значениями времени – зависимые. При построении графиков независимую величину всегда откладывают по горизонтальной оси, а зависимую – по вертикальной.

Функцией называется соответствие между множествами Х и Y, при котором каждому элементу множества Х соответствует единственный элемент множества Y.

Переменную х (элемент множества Х) называют независимой переменной или аргументом, а переменную у (элемент множества Y) – зависимой переменной. Говорят, что у является функцией от х. Если переменная у является функцией от переменной х, то используется запись y=f(x) (читается: «у равен f от х»). Если функция задана выражением с переменной х, то символом f(x) обозначается выражение, которым задаётся эта функция.

Если одновременно рассматриваются несколько функций, то для их обозначения используются и другие буквы латинского или греческого алфавитов. Например, буквы g, h, φ.

Множество значений аргумента (значения х, при которых функция будет иметь смысл) называют областью определения функции. Если задаётся функция, то указывается правило соответствия и область её определения. Если функция задана формулой и её область определения не указана, то считают, что она совпадает с областью допустимых значений аргумента. Например, областью определения функции f(x)=x²-2x является множества всех чисел. А областью определения функции 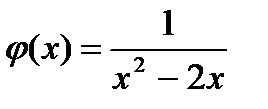 является множество всех чисел, кроме 0 и 2.

В формулу S=a² вместо переменной а можно подставить любое число. Однако если речь идёт о площади квадрата S как функции его стороны а, то областью определения этой функции является множество положительных чисел.

Область определения функции y=f(x) принято обозначать символом D(f) или D(y).

Используя эти обозначения, область определения функции f(x)=x²-2x можно записать так: D(f)= .

А область определения функции 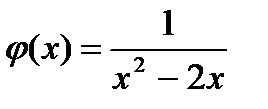 так: D(y)= .

Все значения, которые принимает функция, называют областью значений функции.

Для области значений функции у=f(x) принято обозначение Е(f) или Е(у).

Например, для функции f(x)=x², где -3≤х≤3, областью значений служит промежуток [0;9], т.е. E(f)=[0;9].

Значения аргумента, при которых функция у=f(x) обращается в нуль, называют нулями функции. Промежутки, в которых функция принимает только положительные или только отрицательные значения, называют промежутками знакопостоянства.

В различных областях науки и техники часто встречаются функции, которые называют квадратичными. Например, площадь квадрата у со стороной х, или если тело брошено вверх со скоростью v, то расстояние s от него до поверхности земли в момент времени t определяется формулой , где s₀ – расстояние от тела до поверхности земли в момент времени t=0.

В этих примерах рассмотрены функции вида y=ax²+bx+c.

Функция вида y=ax²+bx+c, где a, b, c – заданные действительные числа, а≠0, х – действительная переменная, называется квадратичной функцией.

Например, квадратичными являются функции: y= x ², y= –2 x ², y= x ² – x, y= x ² –5 x +6, y= .

Рассмотрим функцию у=х², т.е. квадратичную функцию y=ax²+bx+c при а=1, b=с=0. Для построения графика этой функции составим таблицу некоторых её значений.

х	-4	-3	-2	-1	0	1	2	3	4
у=х2	16	9	4	1	0	1	4	9	16

Построив указанные в таблице точки и соединив их плавной кривой, получим график функции у=х². Кривая, являющаяся графиком функции у=х², называется параболой.

Рассмотрим свойства функции у=х². Для этого внимательно прочтём график функции.

Значение функции у=х² положительно при х≠0 и равно нулю при х=0. Можно увидеть, что парабола у=х² проходит через начало координат, а остальные точки параболы лежат выше оси абсцисс. Говорят, что парабола у=х² касается оси абсцисс в точке (0;0).

График функции у=х² симметричен относительно оси ординат. Таким образом, ось ординат является осью симметрии параболы. Точку пересечения параболы с её осью симметрии называют вершиной параболы. Для параболы у=х² вершиной является начало координат.

Сравним графики функций у=2х² и у=х². Составим таблицы значений этих функций.

х	-4	-3	-2	-1	0	1	2	3	4
у=х2	16	9	4	1	0	1	4	9	16
у=2х2	32	18	8	2	0	2	8	19	32

При одном и тои же х значение функции у=2х² в 2 раза больше значения функции у=х². Это значит, что каждую точку графика у=2х² можно получить из точки графика функции у=х² с той же абсциссой увеличением её ординаты в 2 раза.

Говорят, что график функции у=2х² получается растяжением графика функции у=х² от оси Ох вдоль оси Оу в 2 раза.

В то же время можно заметить, что график функции  получается сжатием графика функции у=х² к оси Ох вдоль оси Оу в 2 раза.

Сравним функции у= –х² и у=х². При одном и том же х значения этих функций равны по модулю и противоположны по знаку. Следовательно, график функции у= –х² можно получить симметрией относительно оси Ох графика функции у=х². Аналогично график функции  симметричен графику функции относительно оси Ох.

График функции у=ах² при любом а≠0 также называют параболой. При а>0 ветви параболы направлены вверх, а при a<0 – вниз.

Рассмотрим график и свойства функции . Для этого нам сначала нужно вспомнить функцию, называемой прямой пропорциональностью. Прямая пропорциональность – это функция, которую можно задать формулой y=kx, где k – не равное нулю число. Почему эта функция называется пропорциональностью? Потому что у изменяется пропорционально изменению х. При k>0 во сколько раз увеличивается х, во столько же раз увеличивается и у.

Функции  прямо пропорциональна числам, обратным значениям х. Здесь х стоит в знаменателе дроби. А мы уже знаем, что в дроби, чем больше знаменатель, тем меньше дробь и наоборот, чем меньше знаменатель, тем больше дробь. То есть функцию  называют обратной пропорциональностью. Во сколько раз увеличивается х, во столько же раз уменьшается у, и во сколько раз уменьшается х, во столько же раз увеличивается у. При этом k≠0. Число k называют коэффициентом обратной пропорциональности.

Областью определения функции, заданной формулой , является множество действительных чисел, отличных от нуля, так как выражение имеет смысл при любых х, где х≠0.

Графиком функции обратная пропорциональность является гипербола. При k>0 график функции  получается из графика функции  путём его растяжения от оси х в k раз, если k>1, и его сжатия к оси х в  раз, если 0<k<1. При k<0 график функции  получается из графика функции  в результате симметрии относительно оси х.