Сложение и вычитание выражений, содержащих корень. Применение ФСУ к выражениям, содержащим корень

Сложение и вычитание выражений, содержащих корень, проводится как приведение подобных. То есть можно складывать выражения, содержащие корень с одинаковым подкоренным выражением, но с разным или одинаковым коэффициентом.

Т.е., например,

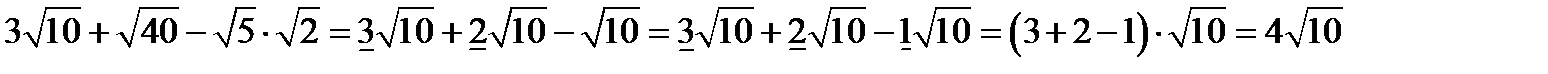
Для применения ФСУ к выражениям, содержащим квадратный корень, нужно устно представить (или заменить) корень вместе с подкоренным выражением как новую переменную и, если получившийся вид нового выражения совпадает с ФСУ, решить это выражение с применением формулы. По окончании решения вернуться к исходному значению корня.

Пример 1

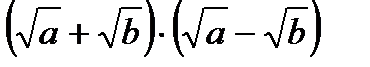
Если мысленно заменить 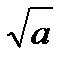на х, а  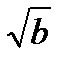на у, то можно увидеть, что в скобках находится сумма и разность двух выражений (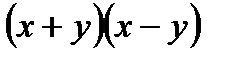), поэтому применяем формулу сокращенного умножения «разность квадратов».

.

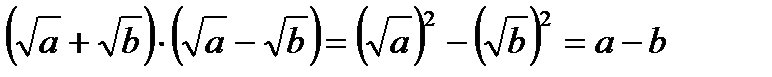Пример 2

Выполнить умножение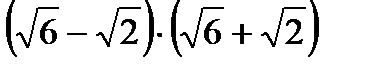  

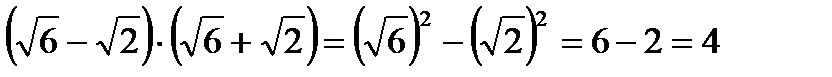
Пример 3

Раскрыть скобки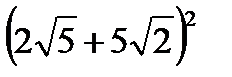

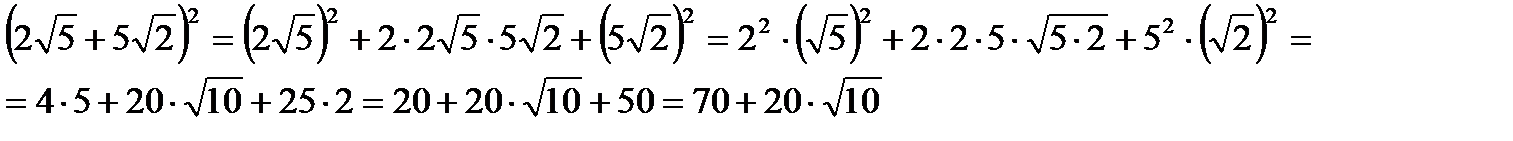
Пример 4

Упростить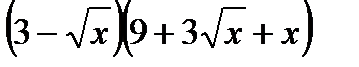

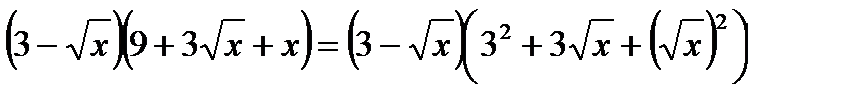
Данное выражение определяет ФСУ «разность кубов»: а³-b³=(a-b)(a²+ab+b²).

То есть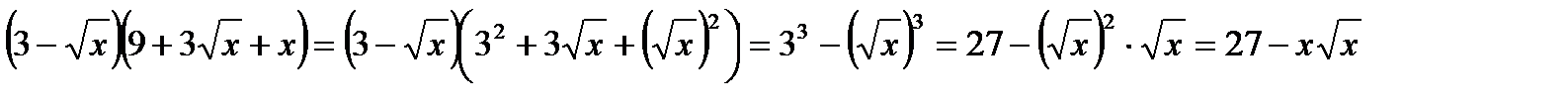

Умножение и деление одночленов и многочленов, содержащих корни

При умножении иррациональных выражений перемножаются их подкоренные числа или выражения:

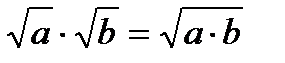
При делении иррациональных выражений подкоренное число или выражение делимого делится на подкоренное число или выражение делителя:

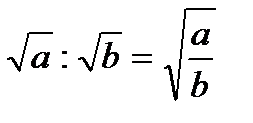
Примеры:

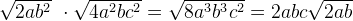
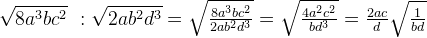
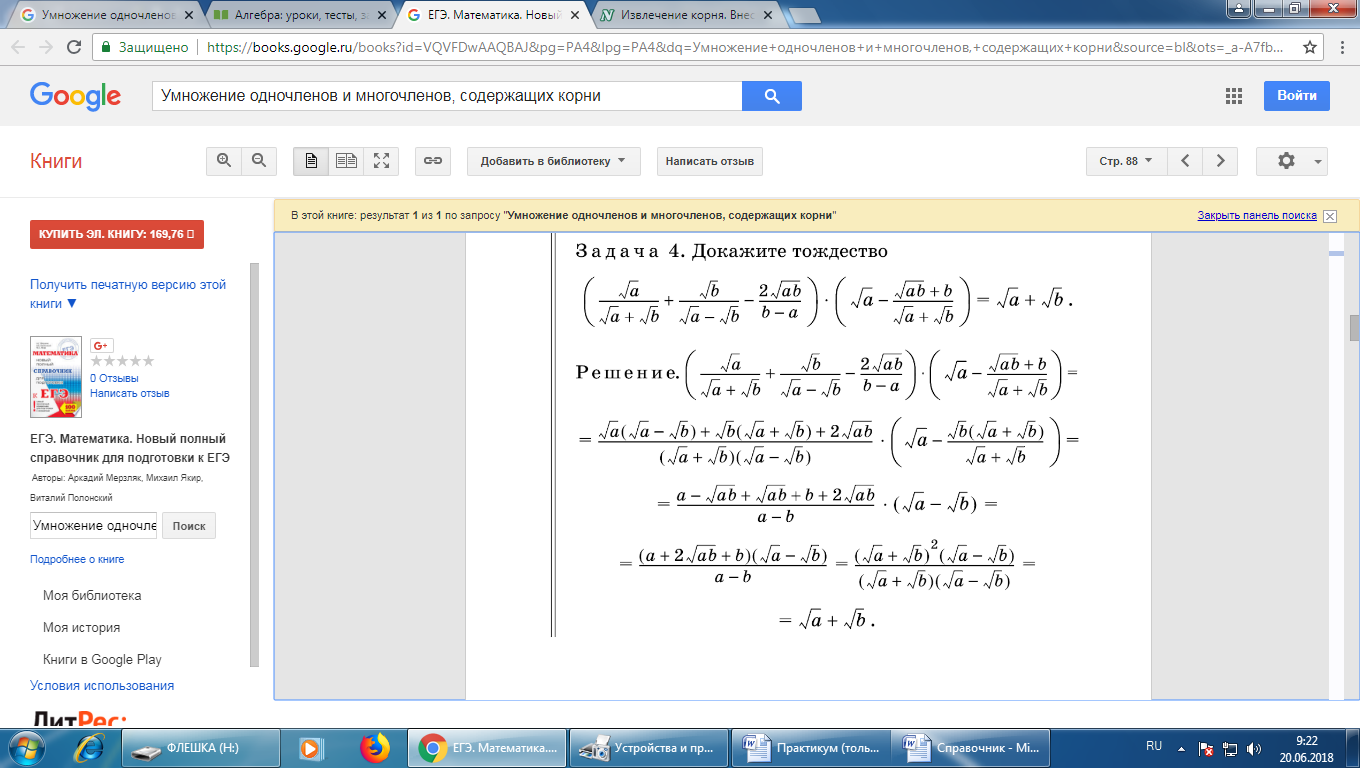
Докажите тождество

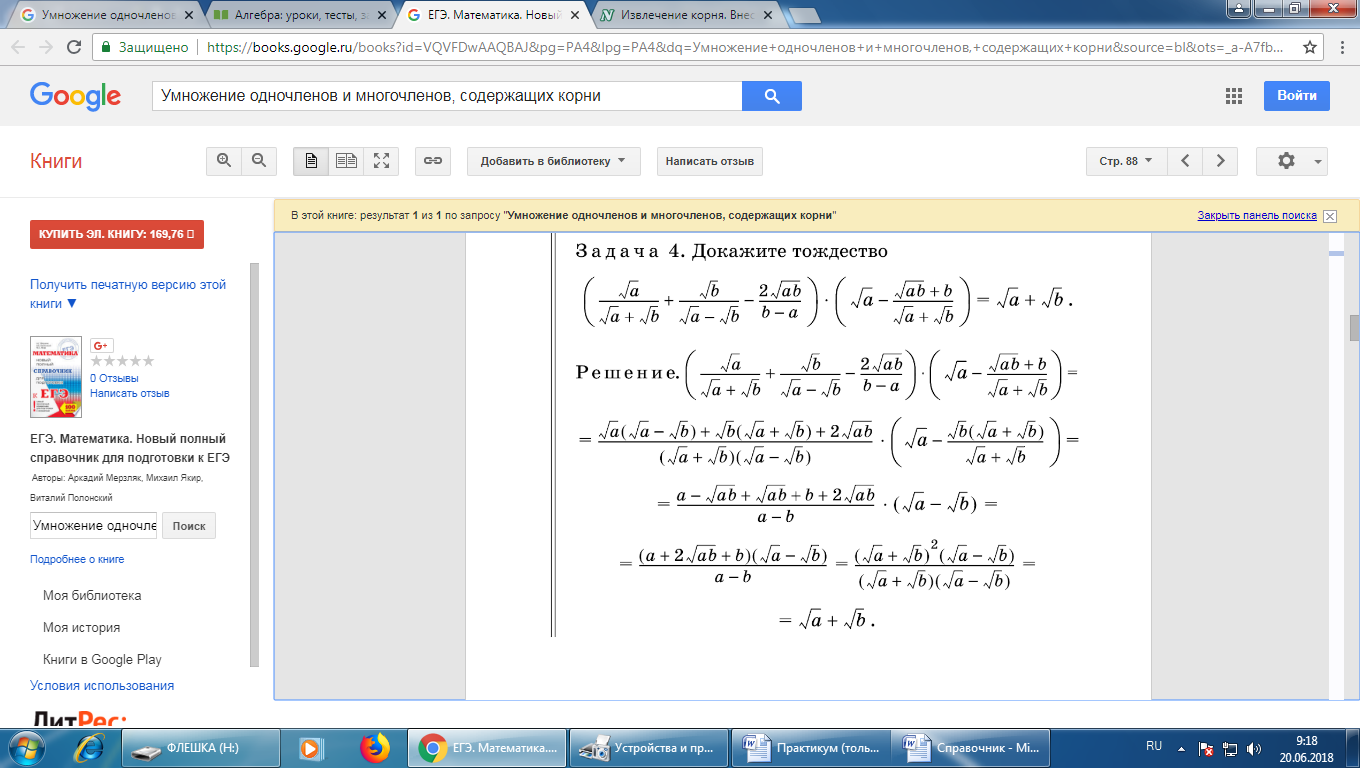
Необходимо в каждой из скобок привести дроби к общему знаменателю. В первой скобке общим знаменателем будет выражение (b-a), представляющее собой разность квадратов 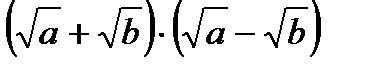. Во второй скобке общим множителем будет выражение .

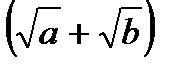Таким образом