2020-06-10
464
Так как согласно определению квадратного корня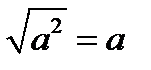 
, то для выполнения операции внесения числа под знак корня можно воспользоваться преобразованием 
.
Для вынесения выражения из-под знака корня нужно подкоренное выражение представить в виде квадрата, а затем вынести получившееся выражение из-под знака корня в соответствии с правилом 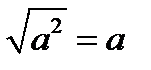. Это же определение квадратного корня в совокупности с формулами сокращённого умножения используют для того, чтобы разложить на множители выражение, содержащее корень.
Пусть требуется упростить выражение 
Для этого представим число 75 в виде произведения, в котором один из множителей является квадратом натурального числа, и применим свойство извлечения корня из произведения. Итак: 
Мы представили 
в виде произведения чисел 5 и 
. В этом случае говорят, что мы вынесли множитель за знак корня.
Теперь упростим исходное выражение: 
.
Для демонстрации процесса внесения под знак корня сравним значения выражений 
и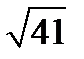 
.
Представим в выражении множитель 2 в виде арифметического квадратного корня и выполним умножение корней. 
Мы заменили произведение выражением 
В таких случаях говорят, что мы внесли множитель под знак корня.
Теперь можно сравнить и 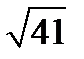. Так как 
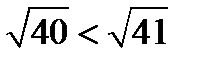, то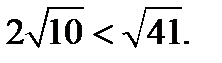 
Под знак корня можно вносить только неотрицательный множитель. Например, выражение 
можно преобразовать, внеся под знак корня множитель 7: 
Выражение 
где с<0, можно преобразовать, внеся под корень положительный множитель – с: 
Представим разложение на множители следующим примером.
Найти наибольшее значение дроби 
.
Представим знаменатель дроби в виде разности квадратов, воспользовавшись тем, что а≥0. Получим: 
Дробь принимает наибольшее значение, когда её знаменатель является наименьшим. Этого можно достичь при а=0. Если а=0, то 
. Значит, наибольшее значение дроби равно 
.
