2020-06-10
376
Очень часто для решения уравнений используется способ замены переменной. Если в уравнение неизвестная входит в состав выражения, повторяющегося в уравнении, то это выражение целиком заменяют на новую переменную. Затем уравнение решают для новой переменной, а затем возвращаются к старой переменной и вновь решают уравнение, но уже для старой переменной.
Рассмотрим следующее уравнение: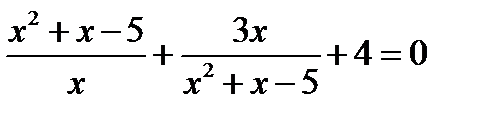 
.
Если мы немного преобразуем это уравнение, то легко заметим повторяющееся выражение, в состав которого входит переменная х.
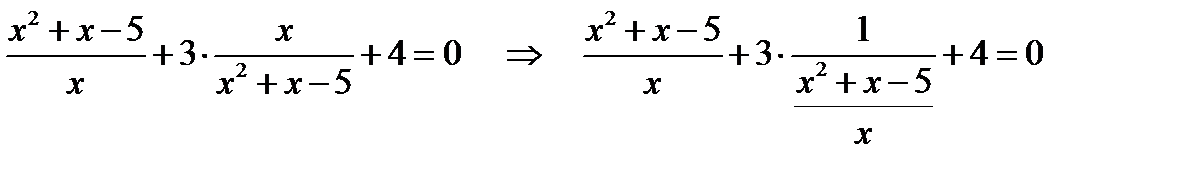
В уравнение неизвестная х входит в виде выражения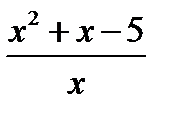 
. Поэтому введём новую переменную 
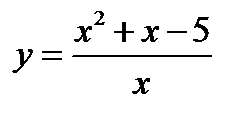. Тогда исходное уравнение примет вид: 
.
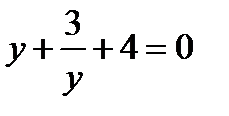ОДЗ у≠0.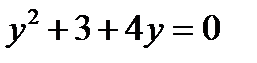 
Найдём дискриминант и корни уравнения
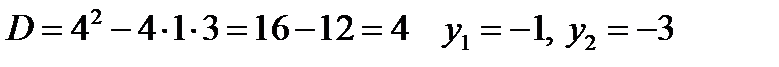
Вернёмся к исходной переменно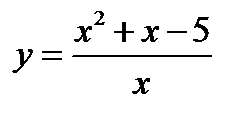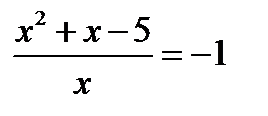й: →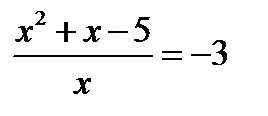 
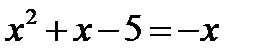и 
и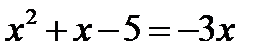 
. Получим 2 квадратных уравнения: 
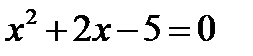и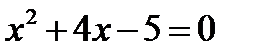 
. Решив их, получим корни: для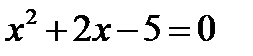 
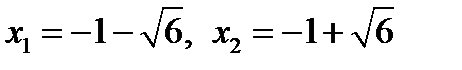, а для уравнения 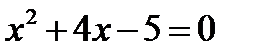корни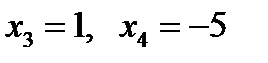 
.
То есть исходное уравнение 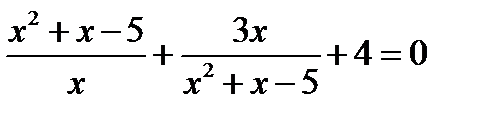имеет 4 корня: , .
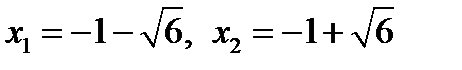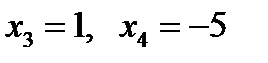Метод введения новой переменной используется также для решения биквадратных и иррациональных уравнений.
|
|
|
Уравнение вида ax 4 + bx 2 + c = 0, где a, b и c — некоторые числа, x — переменная, причем a ≠ 0, называется биквадратным уравнением. Биквадратное уравнение ax 4+ bx 2+ c =0 заменой x 2 = t сводится к квадратному.
Решим уравнение: 9 s 4 + 26 s 2 − 3 = 0.
Пусть s 2 = a. Тогда 9 a 2 + 26 a − 3 = 0. Отсюда a = −3 или a =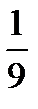 
.
Значит, s 2 = −3 или s 2 = .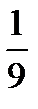
Уравнение s 2 = −3 не имеет корней.
Корнями уравнения s 2 = 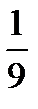являются числа 
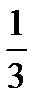и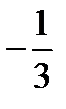 
.
Ответ: s 1 = − 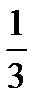; s 2 = .
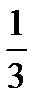С помощью замены можно решать и некоторые другие уравнения.
Решим уравнение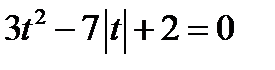 
Пусть |t|=y. Тогда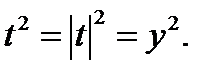 
Это позволяет данное уравнение заменить уравнением 
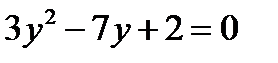, корнями которого являются числа: 
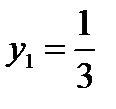и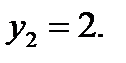 
Вернёмся к исходной переменной t. При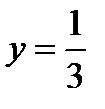 
получаем 
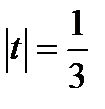. Отсюда получаем 2 корня: 
.
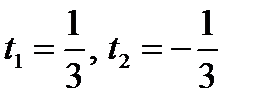Если y = 2, то | t| = 2.
Это дает еще два корня: t 3 = −2, t 4 = 2.
Ответ: −2, 2, 
.
