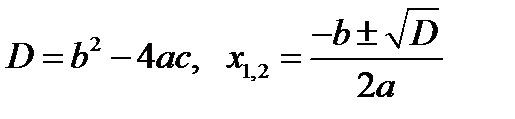Решение квадратных уравнений по формулам

 

.

Есть определённый алгоритм для решения квадратного уравнения полного вида.

1. Определить коэффициенты уравнения.

2. Подставить значения коэффициентов в формулу дискриминанта.

3. Определить количество корней квадратного уравнения.

Если D>0, то уравнение имеет 2 корня.

Если D=0, то уравнение имеет один корень.

Если же D<0, то уравнение корней не имеет.

4. Найти корни либо записать, что корней нет.

Если D>0, то уравнение имеет 2 корня .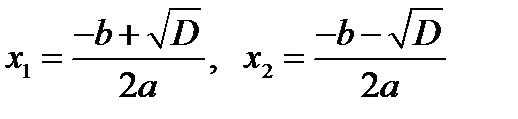

Если D=0, то уравнение имеет один корень .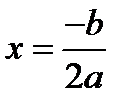

5. При необходимости проверить корни, подставив их в исходное уравнение.

 

Решим несколько квадратных уравнений для примера.

      Коэффициенты:

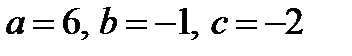
Вычислим дискриминант: 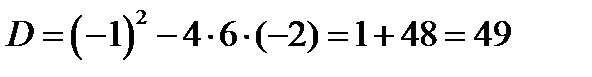, т.е. D>0.

Уравнение имеет 2 корня.

Найдём корни уравнения: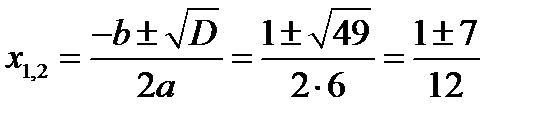

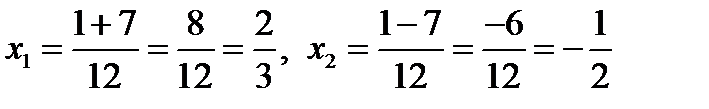
Проверка: Подставим корни  в уравнение

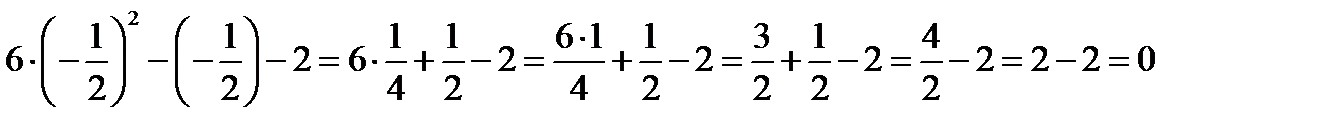
Ответ: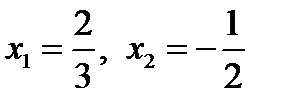

 

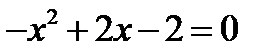 Это уравнение неприведённое, для облегчения решения поменяем знаки всех членов уравнения на противоположные, умножив обе части на –1. Получим уравнение 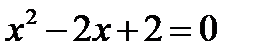, коэффициенты которого .

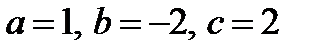Найдём дискриминант: D=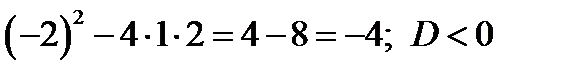

Значит, наше уравнение не имеет корней.

Ответ: корней нет.

 

Преобразуем уравнение так, чтобы его коэффициенты стали целыми числами. Для этого умножим обе его части на 100. Получим 100х²+20х+1=0.

Определим коэффициенты: .

Найдём дискриминант: 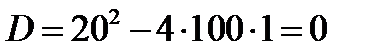. Уравнение имеет один корень.

По формуле находим корень .

Проверка: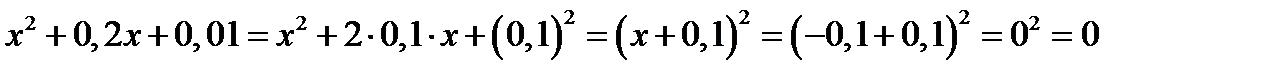

Ответ:

 

Тема 24. Рациональные уравнения