Тема 25. Другие формулы корней квадратных уравнений

и формула корней

Квадратные уравнения, у которых второй коэффициент – чётное число, удобно решать по формуле корней, записанной в другом, более простом виде.

Рассмотрим квадратное уравнение, которое имеет вид ax ²+2 kx + c =0, где k – целое число. Найдём его дискриминант: .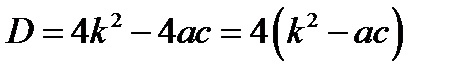

Введём новое обозначение: .

Если D₁>0, то по общей формуле корней квадратного уравнения будем иметь

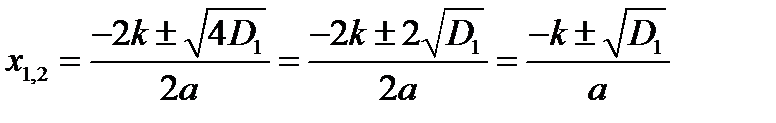Можно заметить, что если заменить ax ²+2 kx + c =0 на выражение ax ²+ bx + c =0, то b =2 k. Отсюда k = . Если вернутся к общему виду квадратного уравнения ax ²+b x + c =0, то получим следующую формулу , где D₁= . Её называют формулой корней квадратного уравнения с чётным вторым коэффициентом.

При D₁=0, корень, по-прежнему находится по формуле х = , а при D₁<0 уравнение корней не имеет.

Для примера решим уравнение .

. x₁=1;

Теорема Виета

Между корнями приведённого квадратного уравнения и его коэффициентами существует определённая связь. Давайте её проследим с помощью некоторых примеров.

Уравнение	Корни	Сумма корней	Произведение корней
	2 и 3	5	6
	– 3 и – 4	– 7	12
	– 1 и 5	4	– 5

Сравнив сумму и произведение корней каждого уравнения с его коэффициентами, можно обнаружить, что в каждом случае сумма корней противоположна коэффициенту при х, а их произведение равно свободному члену. Этим свойством обладает любое приведённое квадратное уравнение, имеющее корни. Справедливо следующее утверждение: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Это утверждение носит название теоремы Виета.

Итак, подведём итог.

Приведённое квадратное уравнение принято записывать так: . Тогда связь корней квадратного уравнения с коэффициентами можно выразить следующим образом: и . Эти формулы называют формулами Виета.

Разделив обе части неприведённого квадратного уравнения на а, получим приведённое квадратное уравнение с теми же корнями. Значит, мы можем применить теорему Виета и для неприведённого квадратного уравнения.

В некоторых случаях можно, используя теорему Виета, подобрать корни, не прибегая к формуле корней.

Решим в качестве примера уравнение Число 15 можно получить перемножением целых чисел только одним способом, если х₁=5, а х₂=3. А сумма 5+3 действительно равна 8.