Задачи на работу и изменение дробей

Самые распространённые задачи на работу – это задачи про бассейны и задачи про изготовление деталей. Решим одну такую задачу.

Один кран наполняет бассейн на 6 часов быстрее другого. Два крана, работая вместе, наполняют бассейн за 4 часа. За сколько часов может наполнить бассейн каждый кран, работая отдельно?

Пусть один кран наполнит бассейн за х ч, тогда другой кран – за (х+6) ч. Пусть объём бассейна составляет V л. Тогда первый кран в час наливает в бассейн л воды, второй кран наливает в час 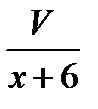л. Вместе в час они наливают л. С другой стороны эти краны наполняют бассейн за 4 ч и в час наливают в него 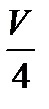л воды. Поэтому получаем рациональное уравнение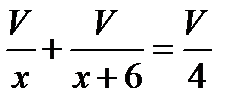

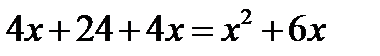Разделим все члены уравнения на V и получим: . Умножим обе части уравнения на общий знаменатель дробей 4 х (х +6) и получим: , или , или 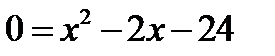. Корни этого квадратного уравнения х₁=6 и х₂= – 4.

Итак, один кран заполнит бассейн за 6 ч, тогда другой кран – за 6+6=12 ч.

Решим ещё одну задачу. Знаменатель несократимой обыкновенной дроби больше её числителя на 5. Если и числитель и знаменатель увеличить на 2, то полученная дробь будет больше первоначальной на 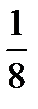. Найдите первоначальную дробь.

Пусть числитель данной дроби равен х, тогда её знаменатель равен х+5 и дробь имеет вид 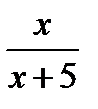. После увеличения на 2 числитель дроби стал равен х+2, знаменатель х+7. Полученная дробь имеет вид 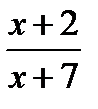. По условию новая дробь больше данной на 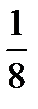. Поэтому имеем рациональное уравнение . Решим его.

Умножим все члены уравнения на общий знаменатель дробей 8(х+7)(х+5) и получим: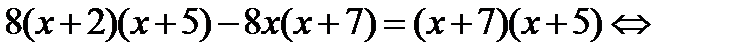

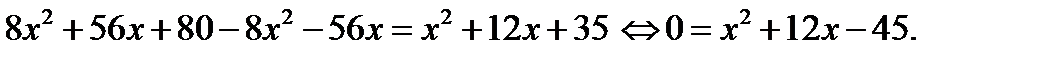
Корни этого квадратного уравнения Итак, числитель дроби 3, её знаменатель равен 3+5=8. Тогда данная дробь равна .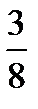

Задачи на сплавы

К сплаву меди и цинка, содержащему 19 кг цинка, добавили 20 кг цинка. В результате содержание меди в сплаве уменьшилось на 25%. Какова была первоначальная масса сплава?

Пусть первоначальная масса сплава была равна х кг. Тогда меди в нём было 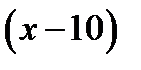кг и она составляла 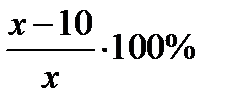от массы сплава. Масса нового сплава, полученного после добавления 20 кг цинка, оказалась равной (х+20) кг, а медь в нём составила 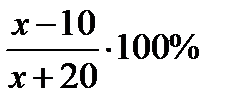. По условию задачи содержание меди уменьшилось на 25%. Следовательно, 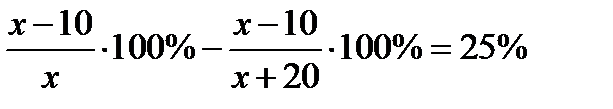. Отсюда .