Виды иррациональных уравнений и их решение

 

Иррациональными называются уравнения, в которых переменная содержится под знаком корня.

Иррациональные уравнения могут быть также решены путем возведения обеих частей уравнения в натуральную степень. При возведении уравнения в степень могут появиться посторонние корни. Поэтому необходимой частью решения иррационального уравнения является проверка.

При решении иррациональных уравнений следует помнить несколько ограничений:

1) Выражение под корнем четной степени должно быть неотрицательным (т.е. больше или равным нуля).

2) Корень четной степени может принимать только неотрицательные значения.

Почти каждое уравнение можно решать двумя подходами:

А) найти область допустимых значений (ОДЗ) для переменной и проверить, входят ли в эту область полученные корни,

Б) решать «в лоб», но для всех полученных корней сделать проверку, подставив их в исходное уравнение.

Но в любом случае, всегда следует стараться сделать проверку. Иногда это затруднительно, особенно если корень получился похожим на нечто такое: , но пробовать стоит всегда.

Для того, чтобы показать необходимость проверки полученных корней, рассмотрим два равенства: 2=2 и –2 =2.

Первое из них верное, а второе – нет.

Возведем обе части каждого из них в квадрат.

Получим 4=4 и 4=4.

Получено два верных равенства.

Из этого бесхитростного примера можно сделать вывод: при возведении в квадрат обеих частей уравнения нередко появляются лишние корни, т.к. при возведении в квадрат отрицательные величины становятся положительными.

Алгоритм решения уравнений вида: .

1) Найти область допустимых значений переменной, решив систему неравенств

2) Возвести в квадрат обе части уравнения, тем самым избавиться от корня.

3) Решить полученное уравнение:

4) Проверить, входят ли полученные корни в область допустимых значений.

5) Сделать проверку корней, подставив их в исходное уравнение.

Пример 1 (Уравнение имеет корни):

ОДЗ:

Возведём обе части уравнения в квадрат

, значит, не является корнем уравнения, т.к. не входит в ОДЗ.

Корень уравнения 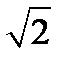. Проверим этот корень, подставив его в исходное равенство.

Преобразуем левую часть

Получили верное равенство 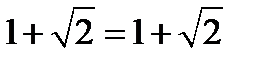, значит, является корнем уравнения.

Ответ:

Пример 2 (уравнение корней не имеет):

Эта система не имеет решения, так как не существует таких чисел, которые одновременно были больше 8, но меньше 5. Получается, что область допустимых значений не содержит ни одного элемента, т.е. ни одно из значений переменной х не может быть корнем этого уравнения. На этом решение окончено.

Ответ: корней нет.

Замечание: Основной метод решения иррациональных уравнений – возведение обеих частей равенства в степень, равную степени корня, дабы от оного избавиться. Но есть еще замены, преобразования, сокращения и т.д. и т.п.